Тригонометрийн функц агуулсан тэгш бус байдлыг шийдвэрлэхдээ cos(t)>a, sint(t)=a болон ижил төстэй хэлбэрийн хамгийн энгийн тэгш бус байдал руу буулгана. Мөн хамгийн энгийн тэгш бус байдлыг аль хэдийн шийдсэн. Ингээд харцгаая янз бүрийн жишэээнгийн тригонометрийн тэгш бус байдлыг шийдвэрлэх арга замууд.
Жишээ 1. sin(t) > = -1/2 тэгш бус байдлыг шийд.
Нэгж тойрог зур. Тодорхойлолтоор sin(t) нь у координат тул Ой тэнхлэгт y = -1/2 цэгийг тэмдэглэнэ. Үхрийн тэнхлэгтэй параллель түүгээр бид шулуун шугам зурна. Нэгж тойргийн графиктай шулуун шугамын огтлолцол дээр Pt1 ба Pt2 цэгүүдийг тэмдэглэнэ. Бид координатын эхийг Pt1 ба Pt2 цэгүүдтэй хоёр сегментээр холбодог.
Энэ тэгш бус байдлын шийдэл нь эдгээр цэгүүдийн дээр байрлах нэгж тойргийн бүх цэгүүд байх болно. Өөрөөр хэлбэл, шийдэл нь l нум байх болно. Одоо дурын цэг l нуманд хамаарах нөхцлийг зааж өгөх шаардлагатай.
Pt1 баруун хагас тойрогт оршдог, ординат нь -1/2, дараа нь t1=arcsin(-1/2) = - pi/6. Pt1 цэгийг тодорхойлохын тулд та дараах томъёог бичиж болно.
t2 = pi - arcsin(-1/2) = 7*pi/6. Үүний үр дүнд бид t-ийн хувьд дараахь тэгш бус байдлыг олж авна.
Бид тэгш бус байдлыг хадгалдаг. Мөн синус функц нь үе үе байдаг тул шийдлүүд 2*pi тутамд давтагдана гэсэн үг юм. Бид энэ нөхцлийг t-ийн үр дүнд үүссэн тэгш бус байдалд нэмээд хариултыг бичнэ.
Хариулт: -pi/6+2*pi*n< = t < = 7*pi/6 + 2*pi*n, при любом целом n.
Жишээ 2. cos(t) тэгш бус байдлыг шийд<1/2.
Нэгж тойрог зуръя. Тодорхойлолтын дагуу cos(t) нь x координат тул бид Ox тэнхлэг дээрх график дээр x = 1/2 цэгийг тэмдэглэнэ.
Энэ цэгээр бид Oy тэнхлэгтэй параллель шулуун шугам татна. Нэгж тойргийн графиктай шулуун шугамын огтлолцол дээр Pt1 ба Pt2 цэгүүдийг тэмдэглэнэ. Бид координатын гарал үүслийг Pt1 ба Pt2 цэгүүдтэй хоёр сегментээр холбодог.

Шийдлүүд нь l нуманд хамаарах нэгж тойргийн бүх цэгүүд байх болно t1 ба t2 цэгүүдийг олъё.
t1 = arccos(1/2) = pi/3.
t2 = 2*pi - arccos(1/2) = 2*pi-pi/3 = 5*pi/6.
Бид t: pi/3-ийн тэгш бус байдлыг олж авлаа Косинус нь үечилсэн функц тул шийдлүүд 2*pi тутамд давтагдана. Бид энэ нөхцлийг t-ийн үр дүнд үүссэн тэгш бус байдалд нэмээд хариултыг бичнэ. Хариулт: pi/3+2*pi*n Жишээ 3. tg(t) тэгш бус байдлыг шийд< = 1. Шүргэх хугацаа нь pi-тэй тэнцүү байна. (-pi/2;pi/2) зөв хагас тойрогт хамаарах шийдлүүдийг олцгооё. Дараа нь шүргэгчийн үечлэлийг ашиглан бид энэ тэгш бус байдлын бүх шийдлийг бичнэ. Нэгж тойрог зураад түүн дээр шүргэгч шугамыг тэмдэглэе. Хэрэв t нь тэгш бус байдлын шийдэл бол T = tg(t) цэгийн ординат нь 1-ээс бага буюу тэнцүү байх ёстой. Ийм цэгүүдийн олонлог нь AT туяаг бүрдүүлнэ. Энэ цацрагийн цэгүүдэд тохирох Pt цэгүүдийн багц нь l нум юм. Түүнчлэн P(-pi/2) цэг нь энэ нуманд хамаарахгүй. Тэгш бус байдал нь a › b хэлбэрийн харилцаа бөгөөд a ба b нь дор хаяж нэг хувьсагч агуулсан илэрхийлэл юм. Тэгш бус байдал нь хатуу - ‹, › ба хатуу бус - ≥, ≤ байж болно. Тригонометрийн тэгш бус байдал нь F(x) › a, F(x) ‹ a, F(x) ≤ a, F(x) ≥ a хэлбэрийн илэрхийлэл бөгөөд F(x) нь нэг буюу хэд хэдэн тригонометрийн функцээр илэрхийлэгдэнэ. . Хамгийн энгийн тригонометрийн тэгш бус байдлын жишээ бол: sin x ‹ 1/2. Ийм асуудлыг графикаар шийдвэрлэх нь заншилтай бөгөөд үүнд зориулж хоёр аргыг боловсруулсан болно. sin x ‹ 1/2 тэгш бус байдлын нөхцлийг хангах интервалыг олохын тулд та дараах алхмуудыг хийх ёстой. Илэрхийлэлд хатуу тэмдгүүд байгаа бол огтлолцох цэгүүд нь шийдэл биш юм. Синусоидын хамгийн бага эерэг үе нь 2π тул хариултыг дараах байдлаар бичнэ. Хэрэв илэрхийллийн шинж тэмдгүүд нь хатуу биш бол уусмалын интервалыг дөрвөлжин хаалтанд оруулах ёстой - . Асуудлын хариултыг мөн дараах тэгш бус байдлаар бичиж болно. Үүнтэй төстэй асуудлыг тригонометрийн тойрог ашиглан хялбархан шийдэж болно. Хариултыг олох алгоритм нь маш энгийн: Син x › 1/2 тэгш бус байдлын жишээн дээр шийдлийн үе шатуудад дүн шинжилгээ хийцгээе. α ба β цэгүүдийг тойрог дээр тэмдэглэсэн - утгууд α ба β-ээс дээш байрлах нумын цэгүүд нь өгөгдсөн тэгш бус байдлыг шийдвэрлэх интервал юм. Хэрэв та cos-ийн жишээг шийдэх шаардлагатай бол хариултын нум нь OY биш харин OX тэнхлэгт тэгш хэмтэй байрлана. Та текстийн доорх диаграммд нүгэл ба cos-ийн шийдлийн интервалуудын ялгааг авч үзэж болно. Тангенс ба котангентын тэгш бус байдлын график шийдэл нь синус ба косинусын аль алинаас нь ялгаатай байх болно. Энэ нь функцүүдийн шинж чанартай холбоотой юм. Арктангенс ба арккотангенс нь тригонометрийн тойрогтой шүргэгч бөгөөд хоёр функцийн хамгийн бага эерэг үе нь π байна. Хоёрдахь аргыг хурдан бөгөөд зөв ашиглахын тулд нүгэл, cos, tg, ctg утгуудыг аль тэнхлэгт зурсан болохыг санах хэрэгтэй. Шүргэх шүргэгч нь OY тэнхлэгтэй параллель гүйдэг. Хэрэв бид арктан а-ийн утгыг нэгж тойрог дээр зурвал хоёр дахь шаардлагатай цэг нь диагональ хэсэгт байрлана. Өнцөг График нь тэдгээрт чиглэдэг боловч хэзээ ч хүрч чаддаггүй тул тэдгээр нь функцийн таслах цэгүүд юм. Котангентын хувьд шүргэгч нь OX тэнхлэгтэй параллель гүйдэг ба функц нь π ба 2π цэгүүдэд тасалддаг. Хэрэв тэгш бус байдлын функцийн аргументыг зөвхөн хувьсагчаар биш, харин үл мэдэгдэхийг агуулсан бүхэл илэрхийллээр төлөөлдөг бол бид нарийн төвөгтэй тэгш бус байдлын тухай ярьж байна. Үүнийг шийдвэрлэх үйл явц, журам нь дээр дурдсан аргуудаас арай өөр юм. Дараах тэгш бус байдлын шийдлийг олох хэрэгтэй гэж бодъё. График шийдэл нь дур мэдэн сонгосон x утгуудыг ашиглан ердийн y = sin x синусоид байгуулах явдал юм. Графикийн хяналтын цэгүүдийн координат бүхий хүснэгтийг тооцоолъё. Үр дүн нь үзэсгэлэнтэй муруй байх ёстой. Шийдвэр олоход хялбар болгохын тулд нарийн төвөгтэй функцийн аргументыг орлъё Ихэнх оюутнууд тригонометрийн тэгш бус байдалд дургүй байдаг. Гэхдээ дэмий л. Нэг дүрийн хэлсэнчлэн, "Та тэднийг хэрхэн хоол хийхээ мэдэхгүй байна" Тэгэхээр яаж "хоол хийх", синустай тэгш бус байдлыг юугаар оруулах вэ гэдгийг бид энэ нийтлэлээс олж мэдэх болно. Бид үүнийг хамгийн энгийн аргаар шийдэх болно - нэгжийн тойрог ашиглан. Тиймээс юуны түрүүнд бидэнд дараах алгоритм хэрэгтэй. Чухал: dөгөгдсөн алгоритм ажиллахгүй байна$\sin(x) > 1 хэлбэрийн тэгш бус байдлын хувьд; \ \sin(x) \geq 1, \ \sin(x)< -1, \ \sin{x} \leq -1$. В строгом случае эти неравенства не имеют решений, а в нестрогом – решение сводится к решению уравнения $\sin{x} = 1$ или $\sin{x} = -1$. Дээр дурдсан алгоритмыг ашиглахгүйгээр логикоор шийдвэрлэхэд илүү тохиромжтой дараах тохиолдлуудыг тэмдэглэх нь зүйтэй. Онцгой тохиолдол 1.Тэгш бус байдлыг шийдвэрлэх: $\sin(x)\leq 1.$ $y=\sin(x)$ тригонометрийн функцийн утгын хүрээ $1$ модулиас ихгүй байгаа тул тэгш бус байдлын зүүн тал аль ч үедТодорхойлолтын домайнаас $x$ (мөн синусын тодорхойлолтын домэйн нь бүх бодит тоо) $1$-аас ихгүй байна. Тиймээс хариултдаа бид бичнэ: $x \in R$. Үр дагавар: $\sin(x)\geq -1.$ Онцгой тохиолдол 2.Тэгш бус байдлыг шийдвэрлэх: $\sin(x)< 1.$ Тусгай тохиолдол 1-тэй төстэй үндэслэлийг ашигласнаар $\sin(x) = 1$ тэгшитгэлийн шийдэл болох цэгүүдээс бусад бүх $x \ R$-д тэгш бус байдлын зүүн тал $1$-ээс бага байгааг олж мэдэв. Энэ тэгшитгэлийг шийдэхэд бид дараахь зүйлийг авна. $x = (-1)^(n)\arcsin(1)+ \pi n = (-1)^(n)\frac(\pi)(2) + \pi n.$ Тиймээс хариултдаа бид бичнэ: $x \in R \арын налуу зураас \left\((-1)^(n)\frac(\pi)(2) + \pi n\right\)$. Үр дагавар:тэгш бус байдлыг ижил аргаар шийддэг $\sin(x) > -1.$ Жишээ 1:Тэгш бус байдлыг шийдвэрлэх: $\sin(x) \geq \frac(1)(2).$ Тиймээс шийдэл нь дараах хэлбэртэй болно. $x \in \left[\frac(\pi)(6) + 2\pi n; \frac(5\pi)(6) + 2 \pi n\баруун], \n \Z.$-д Жишээ 2:Тэгш бус байдлыг шийдвэрлэх: $\sin(x)< -\frac{1}{2}$ Синусын тэнхлэгт $-\frac(1)(2)$ координатыг тэмдэглээд косинусын тэнхлэгтэй параллель, энэ цэгийг дайран өнгөрөх шулуун шугамыг зуръя. Уулзалтын цэгүүдийг тэмдэглэе. Тэгш бус байдал нь хатуу тул тэд сүүдэрлэхгүй. Тэгш бус байдлын тэмдэг $<$, а, значит, закрашиваем область ниже прямой, т.е. меньший полукруг. Неравенство превращаем в равенство и решаем его: $\sin(x)=-\frac(1)(2)$ $x=(-1)^(n)\arcsin(\left(-\frac(1)(2)\баруун))+ \pi n =(-1)^(n+1)\frac(\pi) )(6) + \pi n$. Цаашид $n=0$ гэж үзвэл бид эхний огтлолцлын цэгийг олно: $x_(1)=-\frac(\pi)(6)$. Манай талбай эхний цэгээс сөрөг чиглэлд явж байгаа бөгөөд энэ нь бид $n$-ийг $-1$-тэй тэнцүү болгож байгаа гэсэн үг юм: $x_(2)=(-1)^(-1+1)\frac(\pi)( 6) + \pi \cdot (-1) = -\pi + \frac(\pi)(6) = -\frac(5\pi)(6)$. $x \in \left(-\frac(5\pi)(6) + 2\pi n; -\frac(\pi)(6) + 2 \pi n\right), \n \in Z.$ Жишээ 3:Тэгш бус байдлыг шийдвэрлэх: $1 – 2\sin(\left(\frac(x)(4)+\frac(\pi)(6)\баруун)) \leq 0.$ Энэ жишээг алгоритм ашиглан шууд шийдвэрлэх боломжгүй. Эхлээд та үүнийг өөрчлөх хэрэгтэй. Бид тэгшитгэлээр хийх зүйлээ яг таг хийдэг, гэхдээ тэмдгийг мартаж болохгүй. Сөрөг тоогоор хуваах эсвэл үржүүлэх нь эсрэгээрээ! Тиймээс тригонометрийн функц агуулаагүй бүх зүйлийг баруун тийш шилжүүлье. Бид авах: $- 2\sin(\left(\frac(x)(4)+\frac(\pi)(6)\баруун)) \leq -1.$ Зүүн ба баруун талыг $-2$-оор хуваацгаая (тэмдэгтийн талаар бүү март!). Бидэнд байх болно: $\sin(\left(\frac(x)(4)+\frac(\pi)(6)\баруун)) \geq \frac(1)(2).$ Дахиад бид алгоритм ашиглан шийдэж чадахгүй тэгш бус байдалтай байна. Гэхдээ энд хувьсагчийг өөрчлөхөд хангалттай: $t=\frac(x)(4)+\frac(\pi)(6).$ Бид дараах алгоритмыг ашиглан шийдэж болох тригонометрийн тэгш бус байдлыг олж авна. $\sin(t) \geq \frac(1)(2).$ Энэ тэгш бус байдлыг жишээ 1-д шийдсэн тул эндээс хариултыг зээлж авъя: $t \in \left[\frac(\pi)(6) + 2\pi n; \frac(5\pi)(6) + 2 \pi n\баруун].$ Гэсэн хэдий ч шийдвэр хараахан дуусаагүй байна. Бид анхны хувьсагч руугаа буцах хэрэгтэй. $(\frac(x)(4)+\frac(\pi)(6)) \left[\frac(\pi)(6) + 2\pi n; \frac(5\pi)(6) + 2 \pi n\баруун].$ Интервалыг системээр төсөөлье: $\left\(\begin(массив)(c) \frac(x)(4)+\frac(\pi)(6) \geq \frac(\pi)(6) + 2\pi n, \\ \frac(x)(4)+\frac(\pi)(6) \leq \frac(5\pi)(6) + 2 \pi n \end(массив) \right.$ Системийн зүүн талд интервалд хамаарах илэрхийлэл ($\frac(x)(4)+\frac(\pi)(6)$) байна. Интервалын зүүн хил нь эхний тэгш бус байдлыг хариуцдаг бол баруун талын хил нь хоёр дахь тэгш бус байдлыг хариуцна. Түүнээс гадна хаалт нь чухал үүрэг гүйцэтгэдэг: хэрэв хаалт нь дөрвөлжин байвал тэгш бус байдал тайвширч, дугуй байвал хатуу байх болно. Бидний даалгавар бол зүүн талаас $x$ авах явдал юм тэгш бус байдлын аль алинд нь. $\frac(\pi)(6)$-г зүүн талаас баруун тийш шилжүүлбэл бид дараахыг авна. $\left\(\begin(массив)(c) \frac(x)(4) \geq \frac(\pi)(6) + 2\pi n -\frac(\pi)(6), \\ \frac(x)(4) \leq \frac(5\pi)(6) + 2 \pi n – \frac(\pi)(6) \end(массив) \баруун.$. Хялбаршуулж, бид дараах байдалтай байна: $\left\(\begin(массив)(c) \frac(x)(4) \geq 2\pi n, \\ \frac(x)(4) \leq \frac(2\pi)(3) + 2 \pi n \end(массив) \right.$ Зүүн ба баруун талыг 4 доллараар үржүүлбэл бид дараахь зүйлийг авна. $\left\(\begin(массив)(c) x \geq 8\pi n, \\ x \leq \frac(8\pi)(3) + 8 \pi n. \end(массив) \баруун. доллар Системийг интервалд угсарснаар бид дараах хариултыг авна. $x \in \left[ 8\pi n; \frac(8\pi)(3) + 8 \pi n\баруун], \n \Z.$-д ТРИГОНОМЕТРИЙН ТЭГШ БУС БАЙДЛЫГ ШИЙДЭХ АРГА
Хамааралтай байдал.
Түүхээс харахад тригонометрийн тэгшитгэл, тэгш бус байдлыг сургуулийн сургалтын хөтөлбөрт онцгой байр суурь эзэлдэг. Тригонометр бол сургуулийн хичээл, ерөнхийдөө математикийн шинжлэх ухааны хамгийн чухал хэсгүүдийн нэг гэж бид хэлж чадна. Тригонометрийн тэгшитгэл ба тэгш бус байдал нь ерөнхий боловсролын сургуулийн математикийн хичээлд агуулгын хувьд гол байруудын нэгийг эзэлдэг. боловсролын материал, мөн суралцах явцад бий болох, хэрэгжүүлэх ёстой боловсролын болон танин мэдэхүйн үйл ажиллагааны аргуудын дагуу онолын болон хэрэглээний шинж чанартай олон тооны асуудлыг шийдвэрлэхэд ашиглаж болно. Тригонометрийн тэгшитгэл ба тэгш бус байдлыг шийдвэрлэх нь тригонометрийн бүх сургалтын материалтай холбоотой оюутнуудын мэдлэгийг системчлэх урьдчилсан нөхцөлийг бүрдүүлдэг (жишээлбэл, тригонометрийн функцүүдийн шинж чанар, тригонометрийн илэрхийлэлийг хувиргах аргууд гэх мэт) бөгөөд судалж буй материалтай үр дүнтэй холбоо тогтоох боломжийг олгодог. алгебр (тэгшитгэл, тэгшитгэлийн эквивалент, тэгш бус байдал, алгебрийн илэрхийллийн ижил хувиргалт гэх мэт). Өөрөөр хэлбэл, тригонометрийн тэгшитгэл ба тэгш бус байдлыг шийдвэрлэх арга техникийг авч үзэх нь эдгээр ур чадварыг шинэ агуулгад шилжүүлэх явдал юм. Онолын ач холбогдол, түүний олон тооны хэрэглээ нь сонгосон сэдвийн хамаарлын нотолгоо юм. Энэ нь эргээд курсын ажлын зорилго, зорилт, судалгааны сэдвийг тодорхойлох боломжийг олгодог. Судалгааны зорилго:
тригонометрийн тэгш бус байдлын боломжит төрлүүд, тэдгээрийг шийдвэрлэх үндсэн ба тусгай аргуудыг нэгтгэн дүгнэх, сургуулийн сурагчдын тригонометрийн тэгш бус байдлыг шийдвэрлэх багц асуудлыг сонгох. Судалгааны зорилго:
1. Судалгааны сэдвээр байгаа уран зохиолын дүн шинжилгээнд үндэслэн материалыг системчлэх. 2. “Тригонометрийн тэгш бус байдал” сэдвийг нэгтгэхэд шаардлагатай багц даалгавруудыг өг. Судалгааны объект
нь сургуулийн математикийн хичээлийн тригонометрийн тэгш бус байдал юм. Судалгааны сэдэв:
тригонометрийн тэгш бус байдлын төрлүүд, тэдгээрийг шийдвэрлэх арга. Онолын ач холбогдол
материалыг системчлэх явдал юм. Практик ач холбогдол:
асуудлыг шийдвэрлэхэд онолын мэдлэгийг ашиглах; тригонометрийн тэгш бус байдлыг шийдвэрлэх үндсэн нийтлэг аргуудын шинжилгээ. Судалгааны аргууд
: шинжлэх ухааны уран зохиолд дүн шинжилгээ хийх, олж авсан мэдлэгийг нэгтгэх, нэгтгэх, асуудлыг шийдвэрлэхэд дүн шинжилгээ хийх, тэгш бус байдлыг шийдвэрлэх оновчтой аргуудыг хайх. §1.
Тригонометрийн тэгш бус байдлын төрлүүд, тэдгээрийг шийдвэрлэх үндсэн аргууд
1.1. Хамгийн энгийн тригонометрийн тэгш бус байдал
эсвэл > тэмдгээр холбогдсон хоёр тригонометрийн илэрхийллийг тригонометрийн тэгш бус байдал гэнэ. Тригонометрийн тэгш бус байдлыг шийдвэрлэх гэдэг нь тэгш бус байдлыг хангасан тэгш бус байдалд орсон үл мэдэгдэх утгуудын багцыг олохыг хэлнэ. Тригонометрийн тэгш бус байдлын үндсэн хэсгийг хамгийн энгийн шийдэл болгон бууруулж шийддэг. Энэ нь хүчин зүйлчлэл, хувьсагчийг өөрчлөх арга байж болно ( Хамгийн энгийн тэгш бус байдлыг хоёр аргаар шийдэж болно: нэгж тойрог ашиглах эсвэл графикаар. Болъёf(x
- тригонометрийн үндсэн функцүүдийн нэг. Тэгш бус байдлыг шийдэхийн тулд Тэгш бус байдлыг шийдвэрлэх алгоритмын жишээг өгье Тэгш бус байдлыг шийдвэрлэх алгоритм 1. Тооны синусын тодорхойлолтыг томъёолx
нэгж тойрог дээр. 3. Ординатын тэнхлэг дээр цэгийг координатаар тэмдэглэнэа
.
4. Энэ цэгээр OX тэнхлэгтэй параллель шулуун зурж, түүний огтлолцох цэгүүдийг тойрогоор тэмдэглэнэ. 5. Бүх цэгүүд нь ординатаас бага байх тойргийн нумыг сонгоа
.
6. Тойргийн чиглэлийг (цагийн зүүний эсрэг) зааж, интервалын төгсгөлд функцийн үеийг нэмж хариултыг бичнэ үү.2πn
,
Тэгш бус байдлыг шийдвэрлэх алгоритм 1. Тооны шүргэгчийн тодорхойлолтыг томъёолx
нэгж тойрог дээр. 2. Нэгж тойрог зур. 3. Шүргэгчийн шугамыг зурж, ординат бүхий цэгийг тэмдэглэа
.
4. Энэ цэгийг эхтэй холбож, үүссэн сегментийн огтлолцлын цэгийг нэгж тойрогтой тэмдэглэнэ. 5. Бүх цэгүүд нь шүргэгч шулуун дээр ординаттай байхаас бага тойргийн нумыг сонгоа
.
6. Гүйлтийн чиглэлийг зааж, функцийн тодорхойлолтын мужийг харгалзан цэг нэмж хариултыг бичнэ үү.πn
,
Хамгийн энгийн тэгшитгэлийн шийдлийн график тайлбар, тэгш бус байдлыг ерөнхий хэлбэрээр шийдвэрлэх томъёог хавсралтад (Хавсралт 1, 2) үзүүлэв. Жишээ 1.
Тэгш бус байдлыг шийд Нэгж тойрог дээр шулуун шугам зур Бүх утгаy
интервал дээр NM илүү байна
, AMB нумын бүх цэгүүд энэ тэгш бус байдлыг хангаж байна. Бүх эргэлтийн өнцөгт, том Зураг 1 Тиймээс тэгш бус байдлын шийдэл нь интервал дахь бүх утгууд байх болно тэдгээр. Хариулт: 1.2. График арга
Практикт тригонометрийн тэгш бус байдлыг шийдвэрлэх график арга нь ихэвчлэн ашигтай байдаг. Тэгш бус байдлын жишээг ашиглан аргын мөн чанарыг авч үзье 1. Хэрэв аргумент нь төвөгтэй бол (хэрэвX
), дараа нь үүнийг солинот
.
2. Бид нэг координатын хавтгайд бүтээдэгтоглоом
функцын графикууд 3. Бид ийм зүйл олдогграфикуудын огтлолцох хоёр зэргэлдээ цэг, тэдгээрийн хоорондсинус долгионбайрладагилүү өндөр
шууд 4. Аргументийн давхар тэгш бус байдлыг бичт
, косинусын үеийг харгалзан (т
олдсон абсциссуудын хооронд байх болно). 5. Урвуу орлуулалт хийж (анхны аргумент руу буцах) утгыг илэрхийлX
давхар тэгш бус байдлаас бид хариултыг тоон интервал хэлбэрээр бичнэ. Жишээ 2.
Тэгш бус байдлыг шийдэх: . График аргыг ашиглан тэгш бус байдлыг шийдвэрлэхдээ функцүүдийн графикийг аль болох нарийвчлалтай байгуулах шаардлагатай. Тэгш бус байдлыг дараах хэлбэрт шилжүүлье. Нэг координатын систем дэх функцүүдийн графикийг байгуулъя Зураг 2 Функцийн графикууд цэг дээр огтлолцдогА
координатуудтай Хариулт: 1.3. Алгебрийн арга
Ихэнх тохиолдолд анхны тригонометрийн тэгш бус байдлыг зөв сонгосон орлуулалтын тусламжтайгаар алгебрийн (рационал эсвэл иррациональ) тэгш бус байдал болгон бууруулж болно. Энэ арга нь тэгш бус байдлыг хувиргах, орлуулах эсвэл хувьсагчийг орлуулахыг хэлнэ. Энэ аргыг хэрэглэх тодорхой жишээг авч үзье. Жишээ 3.
Хамгийн энгийн хэлбэрт оруулах Зураг 3 Хариулт: Жишээ 4.
Тэгш бус байдлыг шийдвэрлэх: ОДЗ: Томьёог ашиглах: Тэгш бус байдлыг дараах хэлбэрээр бичье. Эсвэл итгэх Сүүлчийн тэгш бус байдлыг интервалын аргаар шийдэж, бид дараахь зүйлийг олж авна. Зураг 4 Зураг 5 Хариулт: 1.4. Интервалын арга
Интервалын аргыг ашиглан тригонометрийн тэгш бус байдлыг шийдвэрлэх ерөнхий схем: Тригонометрийн томьёог ашиглах хүчин зүйл. Функцийн тасалдлын цэг ба тэгийг олж тойрог дээр байрлуул. Ямар ч цэгийг авTO
(гэхдээ өмнө нь олдоогүй) ба бүтээгдэхүүний тэмдгийг олж мэдээрэй. Хэрэв бүтээгдэхүүн эерэг байвал тухайн өнцөгт тохирох туяан дээр нэгж тойргийн гадна цэг тавина. Үгүй бол цэгийг тойрог дотор байрлуулна. Хэрэв цэг хэд хэдэн удаа тохиолдвол бид үүнийг тэгш үржвэрийн цэг гэж нэрлэдэг бол сондгой олон тооны цэг гэж нэрлэдэг. Дараах байдлаар нуман зурна: цэгээс эхэлнэTO
, хэрэв дараагийн цэг нь сондгой үржвэртэй бол нум нь энэ цэг дээр тойрогтой огтлолцдог, харин цэг нь тэгш үржвэртэй бол огтлолцохгүй. Тойргийн ард байгаа нумууд нь эерэг интервалууд юм; тойрог дотор сөрөг орон зай бий. Жишээ 5.
Тэгш бус байдлыг шийдэх Эхний цувралын оноо: Хоёр дахь цувралын оноо: Цэг бүр сондгой олон удаа тохиолддог, өөрөөр хэлбэл бүх цэгүүд сондгой үржвэртэй байдаг. Бүтээгдэхүүний тэмдгийг эндээс олж мэдье Цагаан будаа. 6 Хариулт: Жишээ 6
. Тэгш бус байдлыг шийд.
Шийдэл:
Илэрхийллийн тэгүүдийг олцгооё .
Хүлээн авахaeм :
Нэгж тойргийн цувааны утгууд дээрX
1
цэгээр дүрслэгдсэн Одоо тоогоо өгье Тэгэхээр, цэгА
өнцгийг бүрдүүлж буй цацраг дээр сонгогдох ёстой Одоо цэгээсА
бүх тэмдэглэгдсэн цэгүүд рүү дараалан долгионтой тасралтгүй шугам татна. Мөн цэгүүдэд Зураг 7 Эцсийн хариулт: Анхаарна уу.
Хэрэв долгионы шугамыг нэгж тойрог дээр тэмдэглэсэн бүх цэгүүдийг дайруулсны дараа цэг рүү буцаах боломжгүйА
,
"хууль бус" газар тойргийг гатлахгүйгээр энэ нь шийдэлд алдаа гарсан, тухайлбал сондгой тооны үндэс алга болсон гэсэн үг юм. Хариулт:
.
§2. Тригонометрийн тэгш бус байдлыг шийдвэрлэх бодлогын багц
Сургуулийн сурагчдын тригонометрийн тэгш бус байдлыг шийдвэрлэх чадварыг хөгжүүлэх явцад 3 үе шатыг ялгаж салгаж болно. 1. бэлтгэл, 2. энгийн тригонометрийн тэгш бус байдлыг шийдвэрлэх чадварыг хөгжүүлэх; 3. бусад төрлийн тригонометрийн тэгш бус байдлын танилцуулга. Бэлтгэл үе шатны зорилго нь сургуулийн хүүхдүүдэд тэгш бус байдлыг шийдвэрлэхийн тулд тригонометрийн тойрог эсвэл график ашиглах чадварыг хөгжүүлэх шаардлагатай. Хэлбэрийн энгийн тэгш бус байдлыг шийдвэрлэх чадвар Тоон тойргийн нуман эсвэл функцийн графикийн нумын хувьд давхар тэгш бус байдлыг бий болгох чадвар; Тригонометрийн илэрхийллийн янз бүрийн хувиргалтыг хийх чадвар. Сургуулийн сурагчдын тригонометрийн функцүүдийн шинж чанарын талаархи мэдлэгийг системчлэх явцад энэ үе шатыг хэрэгжүүлэхийг зөвлөж байна. Гол хэрэгсэл нь оюутнуудад санал болгож, багшийн удирдлаган дор эсвэл бие даан гүйцэтгэх даалгавар, мөн тригонометрийн тэгшитгэлийг шийдвэрлэх ур чадвар байж болно. Ийм ажлуудын жишээ энд байна: 1
. Нэгж тойрог дээр цэг тэмдэглэ .
2.
Цэг нь координатын хавтгайн аль дөрөвний нэгт байрладаг вэ? 3.
Тригонометрийн тойрог дээрх цэгүүдийг тэмдэглэ 4.
Илэрхийлэлийг тригонометрийн функц болгон хувиргаIулирал. A) 5.
Arc MR өгөгдсөн.М
- дундI-р улирал,Р
- дундII-р улирал. Хувьсагчийн утгыг хязгаарлахт
хувьд: (давхар тэгш бус байдал гаргах) a) нуман MR; б) RM нумууд. 6.
Графикийн сонгосон хэсгүүдийн давхар тэгш бус байдлыг бичнэ үү. Цагаан будаа. 1 7.
Тэгш бус байдлыг шийдэх 8.
Илэрхийлэл хөрвүүлэх
.
Тригонометрийн тэгш бус байдлыг шийдэж сурах хоёр дахь шатанд бид оюутны үйл ажиллагааг зохион байгуулах арга зүйтэй холбоотой дараах зөвлөмжийг санал болгож болно. Энэ тохиолдолд хамгийн энгийн тригонометрийн тэгшитгэлийг шийдвэрлэх явцад бий болсон тригонометрийн тойрог эсвэл графиктай ажиллах оюутнуудын одоо байгаа ур чадварт анхаарлаа хандуулах шаардлагатай. Нэгдүгээрт, жишээлбэл, хэлбэрийн тэгш бус байдал руу шилжих замаар хамгийн энгийн тригонометрийн тэгш бус байдлыг шийдэх ерөнхий аргыг олж авах нь зүйтэй эсэхийг өдөөж болно. Хоёрдугаарт, багш оюутнуудын анхаарлыг даалгаврыг гүйцэтгэх янз бүрийн аргуудад хандуулж, тэгш бус байдлыг графикаар болон тригонометрийн тойрог ашиглан шийдвэрлэх тохиромжтой жишээг өгөх ёстой. Тэгш бус байдлын дараах шийдлүүдийг авч үзье 1. Нэгж тойргийг ашиглан тэгш бус байдлыг шийдвэрлэх. Тригонометрийн тэгш бус байдлыг шийдвэрлэх эхний хичээлээр бид оюутнуудад тэгш бус байдлыг шийдвэрлэхэд шаардлагатай бүх үндсэн ур чадварыг алхам алхмаар танилцуулах дэлгэрэнгүй алгоритмыг санал болгох болно. Алхам 1.Нэгж тойрог зурж ординатын тэнхлэг дээр цэгийг тэмдэглэе Алхам 2.Энэ шулуун шугам нь тойргийг хоёр нуман болгон хуваасан. -аас их синустай тоог дүрсэлсэн тоог сонгоцгооё Цагаан будаа. 2 Алхам 3.Тэмдэглэгдсэн нумын төгсгөлүүдийн аль нэгийг сонгоно уу. Нэгж тойргийн энэ цэгээр дүрслэгдсэн тоонуудын аль нэгийг бичье Алхам 4.Сонгосон нумын хоёр дахь төгсгөлд тохирох тоог сонгохын тулд бид энэ нумын дагуу нэрлэсэн төгсгөлөөс нөгөө рүү "алхдаг". Үүний зэрэгцээ, цагийн зүүний эсрэг хөдөлж байх үед бидний өнгөрөх тоо нэмэгддэг (эсрэг чиглэлд шилжих үед тоо буурах болно) гэдгийг санаарай. Нэгж тойрог дээр тэмдэглэгдсэн нумын хоёр дахь төгсгөлд дүрслэгдсэн тоог бичье Тиймээс бид тэгш бус байдлыг харж байна Суралцагчдаас зургийг сайтар судалж, тэгш бус байдлын бүх шийдлүүдийн шалтгааныг олж мэдэхийг хүсэх хэрэгтэй Цагаан будаа. 3 Косинусын функцийн тэгш бус байдлыг шийдвэрлэхдээ ординатын тэнхлэгтэй параллель шулуун шугам татдаг болохыг оюутнуудын анхаарлыг татах шаардлагатай. Тэгш бус байдлыг шийдвэрлэх график арга. Бид график бүтээдэг Цагаан будаа. 4 Дараа нь бид тэгшитгэлийг бичнэ (Өгөхn
0, 1, 2 утгууд, бид эмхэтгэсэн тэгшитгэлийн гурван үндэсийг олдог). Үнэ цэнэ Цагаан будаа. 5 Дүгнэж хэлье. Тэгш бус байдлыг шийдэхийн тулд Гуравдугаарт, харгалзах тригонометрийн тэгш бус байдлын язгуурын олонлогийн тухай баримтыг графикаар шийдвэрлэхэд маш тодорхой нотлогддог. Цагаан будаа. 6 Тэгш бус байдлын шийдэл болох эргэлт нь тригонометрийн функцийн үетэй тэнцэх ижил интервалаар давтагдаж байгааг оюутнуудад харуулах шаардлагатай. Та мөн синус функцийн графикийн ижил төстэй дүрслэлийг авч үзэж болно. Дөрөвдүгээрт, тригонометрийн функцүүдийн нийлбэрийг (ялгааг) үржвэр болгон хувиргах техникийг оюутнуудад шинэчлэх ажлыг хийж, тригонометрийн тэгш бус байдлыг шийдвэрлэхэд эдгээр аргуудын үүрэг рольд оюутнуудын анхаарлыг хандуулахыг зөвлөж байна. Ийм ажлыг оюутнууд багшийн санал болгосон даалгаврыг бие даан гүйцэтгэх замаар зохион байгуулж болох бөгөөд үүнд бид дараахь зүйлийг онцолж байна. Тавдугаарт, оюутнуудаас энгийн тригонометрийн тэгш бус байдал бүрийн шийдлийг график эсвэл тригонометрийн тойрог ашиглан дүрслэн харуулахыг шаардах ёстой. Тригонометрийн тэгш бус байдлыг шийдвэрлэхдээ холбогдох зураглал нь өгөгдсөн тэгш бус байдлын шийдлийн багцыг бүртгэх маш тохиромжтой хэрэгсэл болдог тул та түүний зохистой байдалд, ялангуяа тойрог ашиглахад анхаарлаа хандуулах хэрэгтэй. Дараах схемийн дагуу хамгийн энгийн биш тригонометрийн тэгш бус байдлыг шийдвэрлэх аргуудыг оюутнуудад танилцуулахыг зөвлөж байна: тодорхой тригонометрийн тэгш бус байдал руу шилжих, холбогдох тригонометрийн тэгшитгэл рүү шилжих хамтарсан хайлт (багш - оюутнууд) -ийг бие даан шилжүүлэх. ижил төрлийн бусад тэгш бус байдлын аргыг олсон. Тригонометрийн талаархи оюутнуудын мэдлэгийг системчлэхийн тулд бид үүнийг шийдвэрлэх явцад хэрэгжүүлж болох янз бүрийн хувиргалтуудыг шаарддаг ийм тэгш бус байдлыг тусгайлан сонгож, оюутнуудын анхаарлыг тэдгээрийн онцлогт төвлөрүүлэхийг зөвлөж байна. Ийм бүтээмжтэй тэгш бус байдлын хувьд бид жишээлбэл дараахь зүйлийг санал болгож болно. Эцэст нь хэлэхэд бид тригонометрийн тэгш бус байдлыг шийдвэрлэх асуудлын багцын жишээг өгье. 1. Тэгш бус байдлыг шийд: A) б) 5. Тэгш бус байдлын бүх шийдлийг ол: A) ;
б) ;
V) G) г) 6. Тэгш бус байдлыг шийд: A) ;
б) ;
V); G) г); e); ба) 7. Тэгш бус байдлыг шийд: A) б) ;
V); G) . 8. Тэгш бус байдлыг шийд: A) ;
б) ;
V); G) г) e); ба) h) . Математикийн ахисан түвшний суралцаж буй оюутнуудад 6, 7-р даалгаврыг, математикийн гүнзгийрүүлсэн сургалттай ангийн сурагчдад 8-р даалгаврыг санал болгохыг зөвлөж байна. §3. Тригонометрийн тэгш бус байдлыг шийдвэрлэх тусгай аргууд
Тригонометрийн тэгшитгэлийг шийдвэрлэх тусгай аргууд - өөрөөр хэлбэл зөвхөн тригонометрийн тэгшитгэлийг шийдвэрлэхэд ашиглаж болох аргууд. Эдгээр аргууд нь тригонометрийн функцүүдийн шинж чанарыг ашиглах, түүнчлэн янз бүрийн тригонометрийн томьёо, таних тэмдгүүдийг ашиглахад суурилдаг. 3.1. Салбарын арга
Тригонометрийн тэгш бус байдлыг шийдвэрлэх секторын аргыг авч үзье. Маягтын тэгш бус байдлыг шийдвэрлэх Интервалын аргад хэлбэрийн тоо болон хуваагчийн шугаман хүчин зүйл бүрийг Дараахь зүйлийг санаж байх ёстой. a) Маягтын хүчин зүйлүүд б) Маягтын хүчин зүйлүүд Жишээ 1.
Тэгш бус байдлыг шийдэх: a) 3.2. Төвлөрсөн тойрог арга
Энэ арга нь оновчтой тэгш бус байдлын системийг шийдвэрлэх зэрэгцээ тооны тэнхлэгийн аргын аналог юм. Тэгш бус байдлын системийн жишээг авч үзье. Жишээ 5.
Энгийн тригонометрийн тэгш бус байдлын системийг шийд Эхлээд бид тэгш бус байдал бүрийг тусад нь шийддэг (Зураг 5). Зургийн баруун дээд буланд бид тригонометрийн тойргийг аль аргументыг авч үзэхийг зааж өгнө. Зураг 5 Дараа нь бид аргументийн төвлөрсөн тойргийн системийг бий болгодогX
. Бид тойрог зурж, эхний тэгш бус байдлын шийдлийн дагуу сүүдэрлэж, дараа нь илүү том радиустай тойрог зурж, хоёр дахь шийдлийн дагуу сүүдэрлэж, дараа нь бид гурав дахь тэгш бус байдлын тойрог ба суурийн тойрог байгуулна. Бид системийн төвөөс нумануудын төгсгөлд туяа татдаг бөгөөд ингэснээр тэдгээр нь бүх тойрогтой огтлолцдог. Бид үндсэн тойрог дээр уусмал үүсгэдэг (Зураг 6). Зураг 6 Хариулт:
Дүгнэлт
Хичээлийн судалгааны бүх зорилго биелсэн. Онолын материалыг системчилсэн: тригонометрийн тэгш бус байдлын үндсэн төрлүүд ба тэдгээрийг шийдвэрлэх үндсэн аргуудыг (график, алгебр, интервалын арга, сектор ба төвлөрсөн тойргийн арга) өгсөн болно. Арга тус бүрт тэгш бус байдлыг шийдвэрлэх жишээг өгсөн. Онолын хэсгийн дараа практик хэсэг байв. Энэ нь тригонометрийн тэгш бус байдлыг шийдвэрлэх олон даалгавруудыг агуулдаг. Энэхүү курсын ажлыг оюутнууд бие даан ажиллахад ашиглаж болно. Сургуулийн сурагчид энэ сэдвийг эзэмшсэн түвшинг шалгаж, янз бүрийн нарийн төвөгтэй даалгавруудыг гүйцэтгэх дадлага хийх боломжтой. Энэ асуудлын талаархи холбогдох уран зохиолыг судалсны дараа бид сургуулийн алгебр, анхан шатны шинжилгээний хичээлд тригонометрийн тэгш бус байдлыг шийдвэрлэх чадвар, ур чадвар маш чухал бөгөөд үүнийг хөгжүүлэх нь математикийн багшаас ихээхэн хүчин чармайлт шаарддаг гэж бид дүгнэж болно. Иймд энэхүү ажил нь “Тригонометрийн тэгш бус байдал” сэдвээр сурагчдын сургалтыг үр дүнтэй зохион байгуулах боломжийг олгож байгаа тул математикийн багш нарт хэрэг болно. Судалгааг эцсийн мэргэшлийн ажил болгон өргөжүүлэх замаар үргэлжлүүлж болно.
Ашигласан уран зохиолын жагсаалт
Богомолов, Н.В. Математикийн асуудлын цуглуулга [Текст] / N.V. Богомолов. – М .: тоодог, 2009. – 206 х. Выгодский, М.Я. Анхан шатны математикийн гарын авлага [Текст] / М.Я. Выгодский. – М .: тоодог, 2006. – 509 х. Журбенко, Л.Н. Жишээ ба бодлого дахь математик [Текст] / Л.Н. Журбенко. – М.: Инфра-М, 2009. – 373 х. Иванов, О.А. Сургуулийн сурагчид, оюутнууд, багш нарт зориулсан бага ангийн математик [Текст] / О.А. Иванов. – М.: МЦНМО, 2009. – 384 х. Карп, А.П. 11-р ангид эцсийн давталт, баталгаажуулалтыг зохион байгуулах алгебрийн талаархи даалгавар, шинжилгээний эхлэл [Текст] / A.P. Carp. – М.: Боловсрол, 2005. – 79 х. Куланин, Э.Д. Математикийн 3000 уралдааны бодлого [Текст] / Э.Д. Куланин. – М.: Iris-press, 2007. – 624 х. Лейбсон, К.Л. Математикийн практик даалгаврын цуглуулга [Текст] / K.L. Лейбсон. – М .: тоодог, 2010. – 182 х. Тохой, V.V. Параметрүүдтэй холбоотой асуудлууд ба тэдгээрийн шийдэл. Тригонометр: тэгшитгэл, тэгш бус байдал, систем. 10-р анги [Текст] / V.V. Тохой. – М.: АРКТИ, 2008. – 64 х. Манова, А.Н. Математик. Улсын нэгдсэн шалгалтанд бэлтгэх экспресс багш: оюутан. гарын авлага [Текст] / A.N. Манова. – Ростов-на-Дону: Финикс, 2012. – 541 х. Мордкович, А.Г. Алгебр ба математик анализын эхлэл. 10-11 анги. Ерөнхий боловсролын сургуулийн сурагчдад зориулсан сурах бичиг [Текст] / A.G. Мордкович. – М.: Iris-press, 2009. – 201 х. Новиков, А.И. Тригонометрийн функц, тэгшитгэл ба тэгш бус байдал [Текст] / A.I. Новиков. – М.: ФИЗМАТЛИТ, 2010. – 260 х. Оганесян, В.А. Ерөнхий боловсролын сургуульд математикийн хичээл заах арга зүй: Ерөнхий арга зүй. Сурах бичиг физикийн оюутнуудад зориулсан гарын авлага - дэвсгэр. хуурамч. ped. Инст. [Текст] / V.A. Оганесян. – М.: Боловсрол, 2006. – 368 х. Оленик, С.Н. Тэгшитгэл ба тэгш бус байдал. Стандарт бус шийдлийн аргууд [Текст] / С.Н. Оленик. – М.: Факториал хэвлэлийн газар, 1997. – 219 х. Севрюков, П.Ф. Тригонометр, экспоненциал ба логарифм тэгшитгэл ба тэгш бус байдал [Текст] / П.Ф. Севрюков. – М.: Ардын боловсрол, 2008. – 352 х. Сергеев, I.N. Улсын нэгдсэн шалгалт: Математикийн хариулт, шийдэл бүхий 1000 бодлого. C бүлгийн бүх даалгавар [Текст] / I.N. Сергеев. – М.: Шалгалт, 2012. – 301 х. Соболев, А.Б. Анхан шатны математик [Текст] / А.Б. Соболев. – Екатеринбург: Улсын дээд мэргэжлийн боловсролын сургалтын байгууллага USTU-UPI, 2005. – 81 х. Фенко, Л.М. Тэгш бус байдлыг шийдвэрлэх, функцийг судлах интервалын арга [Текст] / L.M. Фенко. – М .: тоодог, 2005. – 124 х. Фридман, Л.М. Математик заах аргын онолын үндэс [Текст] / Л.М. Фридман. – М.: “ЛИБРОКОМ” номын өргөө, 2009. – 248 х. Хавсралт 1 Энгийн тэгш бус байдлын шийдлийн график тайлбар Цагаан будаа. 1 Цагаан будаа. 2 Зураг 3 Зураг 4 Зураг 5 Зураг 6 Зураг 7 Зураг 8 Хавсралт 2 Энгийн тэгш бус байдлын шийдэл Энгийн тригонометрийн тэгш бус байдлыг шийдвэрлэх алгоритм, тригонометрийн тэгш бус байдлыг шийдвэрлэх аргуудыг таних алгоритм. Дээд зэрэглэлийн багш нар: Ширко Ф.М. х Прогресс, МОБУ-6-р дунд сургууль Санкина Л.С. Армавир, "Шинэ зам" хувийн дунд сургууль Байгалийн ухаан, математикийн хичээл заах бүх нийтийн арга байхгүй. Багш бүр зөвхөн өөрт нь л хүлээн зөвшөөрөгдсөн заах арга барилаа олдог. Бидний олон жилийн сургалтын туршлагаас харахад оюутнууд нарийн төвөгтэй сэдвийг сурах эхний шатанд алгоритмыг үйл ажиллагаандаа ашиглахыг зааж өгвөл санах ойд их хэмжээний мэдээллийг төвлөрүүлж, хадгалах шаардлагатай материалыг илүү хялбар сурдаг. Бидний бодлоор ийм сэдэв нь тригонометрийн тэгш бус байдлыг шийдвэрлэх сэдэв юм. Тиймээс бид оюутнуудтай тригонометрийн тэгш бус байдлыг шийдвэрлэх арга техник, аргуудыг тодорхойлохын өмнө хамгийн энгийн тригонометрийн тэгш бус байдлыг шийдвэрлэх алгоритмыг дадлагажуулж, нэгтгэдэг. Энгийн тригонометрийн тэгш бус байдлыг шийдвэрлэх алгоритм
Харгалзах тэнхлэг дээрх цэгүүдийг тэмдэглэ ( Учир нь
нүгэл
x– OA тэнхлэг, хувьдcos
x– ҮХЭР тэнхлэг) Бид тойргийг хоёр цэгээр огтлох тэнхлэгт перпендикулярыг сэргээдэг. Тойрог дээрх эхний цэг нь тодорхойлолтоор нумын функцийн хүрээний интервалд хамаарах цэг юм. Шошгологдсон цэгээс эхлэн тэнхлэгийн сүүдэртэй хэсэгт тохирох тойргийн нумыг сүүдэрлэнэ. Тойрог замын чиглэлд онцгой анхаарал хандуулдаг. Хэрэв эргэлтийг цагийн зүүний дагуу хийвэл (өөрөөр хэлбэл 0-д шилжих шилжилт байгаа бол) тойрог дээрх хоёр дахь цэг нь сөрөг, цагийн зүүний эсрэг байвал эерэг байх болно. Бид хариултыг функцийн үечилсэн байдлыг харгалзан интервал хэлбэрээр бичдэг. Алгоритмын ажиллагааг жишээн дээр авч үзье.
1)
нүгэл
≥ 1/2;
Шийдэл: Бид нэгж тойргийг дүрсэлдэг.; OU тэнхлэг дээр бид ½ цэгийг тэмдэглэнэ. Бид тэнхлэгт перпендикулярыг сэргээж, тойрог хоёр цэг дээр огтлолцдог. Арксинусын тодорхойлолтоор бид эхлээд тэмдэглэж байна π/6 цэг. Тэнхлэгийн тохирох хэсгийг сүүдэрлэнэ өгөгдсөн тэгш бус байдал, ½ цэгээс дээш. Тэнхлэгийн сүүдэртэй хэсэгт тохирох тойргийн нумыг сүүдэрлэнэ. Замын хөдөлгөөнийг цагийн зүүний эсрэг хийж, бид 5π/6 цэгийг авдаг. Бид хариултыг функцийн үечилсэн байдлыг харгалзан интервал хэлбэрээр бичдэг; Хариулт:x;[π/6 + 2π n, 5π/6 + 2π n], n З. Хэрэв хариултын бичлэгт хүснэгтийн утга агуулаагүй бол хамгийн энгийн тэгш бус байдлыг ижил алгоритмаар шийддэг. Оюутнууд эхний хичээлүүд дээрээ самбар дээр тэгш бус байдлыг шийдвэрлэхдээ алгоритмын алхам бүрийг чангаар унш. 2) 5
cos
x
– 1 ≥ 0;
Р 5 cos x – 1 ≥ 0; cos
x ≥ 1/5; Нэгж тойрог зур. Бид OX тэнхлэг дээр 1/5 координат бүхий цэгийг тэмдэглэнэ. Бид тэнхлэгт перпендикулярыг сэргээдэг тойргийг хоёр цэгээр огтолж байна. Тойрог дээрх эхний цэг нь (0;π) тодорхойлолтоор нумын косинусын мужид хамаарах цэг юм. Бид энэ тэгш бус байдалд тохирох тэнхлэгийн хэсгийг сүүдэрлэдэг. Гарын үсэг зурсан цэгээс эхэлнэ
arccos 1/5, тэнхлэгийн сүүдэртэй хэсэгт тохирох тойргийн нумыг сүүдэрлэнэ. Замын хөдөлгөөнийг цагийн зүүний дагуу хийдэг (өөрөөр хэлбэл 0-д шилжих шилжилт байгаа), энэ нь тойрог дээрх хоёр дахь цэг сөрөг байх болно гэсэн үг юм. arccos 1/5. Бид хариултыг функцийн үечилсэн байдлыг харгалзан жижиг утгаас том хүртэл интервал хэлбэрээр бичдэг. Хариулт: x [-arccos 1/5 + 2π n, arccos 1/5 + 2π n], n З. Тригонометрийн тэгш бус байдлыг шийдвэрлэх чадварыг сайжруулахад дараах асуултууд тусалж байна: "Бүлэг тэгш бус байдлыг бид хэрхэн шийдэх вэ?"; "Нэг тэгш бус байдал нөгөөгөөсөө юугаараа ялгаатай вэ?"; "Нэг тэгш бус байдал нөгөөтэй хэрхэн төстэй вэ?"; Хэрэв хатуу тэгш бус байдал өгвөл хариулт хэрхэн өөрчлөгдөх вэ?"; Хэрэв "" тэмдгийн оронд " тэмдэг байвал хариулт хэрхэн өөрчлөгдөх вэ? Тэгш бус байдлын жагсаалтыг тэдгээрийг шийдвэрлэх аргын үүднээс шинжлэх даалгавар нь тэдгээрийг таних дадлага хийх боломжийг олгодог. Оюутнуудад ангид шийдвэрлэх шаардлагатай тэгш бус байдлыг өгдөг. Асуулт:Тригонометрийн тэгш бус байдлыг хамгийн энгийн хэлбэрт оруулахад эквивалент хувиргалтыг ашиглах шаардлагатай тэгш бус байдлыг тодруулна уу? Хариулт 1, 3, 5. Асуулт:Нарийн төвөгтэй аргументыг энгийн гэж үзэх ямар тэгш бус талууд байдаг вэ? Хариулт: 1, 2, 3, 5, 6. Асуулт:Тригонометрийн томъёог ашиглаж болох тэгш бус байдал юу вэ? Хариулт: 2, 3, 6. Асуулт:Шинэ хувьсагчийг нэвтрүүлэх аргыг хэрэглэж болох тэгш бус байдлыг нэрлэнэ үү? Хариулт: 6. Тэгш бус байдлын жагсаалтыг тэдгээрийг шийдвэрлэх аргын үүднээс шинжлэх даалгавар нь тэдгээрийг таних дадлага хийх боломжийг олгодог. Ур чадварыг хөгжүүлэхдээ түүнийг хэрэгжүүлэх үе шатуудыг тодорхойлж, хамгийн энгийн тригонометрийн тэгш бус байдлыг шийдвэрлэх алгоритмд үзүүлсэн ерөнхий хэлбэрээр томъёолох нь чухал юм.Арга 1 - Функцийн графикаар тэгш бус байдлыг шийдвэрлэх
![]()
![]()
Арга 2 - Нэгж тойргийг ашиглан тригонометрийн тэгш бус байдлыг шийдвэрлэх
![]()





Нарийн төвөгтэй тригонометрийн тэгш бус байдал



Синустай тэгш бус байдлыг шийдвэрлэх алгоритм:
Алгоритмын хязгаарлалт
Синустай тэгш бус байдлыг шийдвэрлэх онцгой тохиолдлууд
Алгоритм ашиглан тэгш бус байдлыг шийдвэрлэх жишээ.






 Тиймээс энэ тэгш бус байдлын шийдэл нь интервал байх болно.
Тиймээс энэ тэгш бус байдлын шийдэл нь интервал байх болно.
 ,
,  гэх мэт), ердийн тэгш бус байдлыг эхлээд шийдэж, дараа нь хэлбэрийн тэгш бус байдал
гэх мэт), ердийн тэгш бус байдлыг эхлээд шийдэж, дараа нь хэлбэрийн тэгш бус байдал  гэх мэт, эсвэл бусад аргууд.
гэх мэт, эсвэл бусад аргууд. түүний шийдлийг нэг хугацаанд олоход хангалттай, өөрөөр хэлбэл. урт нь функцийн үетэй тэнцүү аль ч сегмент дээре
x
. Тэгвэл анхны тэгш бус байдлын шийдэл бүгд олдоноx
, түүнчлэн функцийн бүхэл тоогоор олдсон утгуудаас ялгаатай утгууд. Энэ тохиолдолд график аргыг ашиглах нь тохиромжтой.
түүний шийдлийг нэг хугацаанд олоход хангалттай, өөрөөр хэлбэл. урт нь функцийн үетэй тэнцүү аль ч сегмент дээре
x
. Тэгвэл анхны тэгш бус байдлын шийдэл бүгд олдоноx
, түүнчлэн функцийн бүхэл тоогоор олдсон утгуудаас ялгаатай утгууд. Энэ тохиолдолд график аргыг ашиглах нь тохиромжтой. (
(
 ) Мөн
) Мөн  .
.
 (
(
 ).
).
 .
.
 .
.
 (оруултын зүүн талд байгаа тоо нь баруун талд байгаа тооноос үргэлж бага байдаг).
(оруултын зүүн талд байгаа тоо нь баруун талд байгаа тооноос үргэлж бага байдаг). .
.
 , энэ нь тойрогтой А ба В цэгүүдээр огтлолцдог.
, энэ нь тойрогтой А ба В цэгүүдээр огтлолцдог. , гэхдээ бага
, гэхдээ бага  ,
,
 илүү их үнэ цэнийг авах болно
(гэхдээ нэгээс илүүгүй).
илүү их үнэ цэнийг авах болно
(гэхдээ нэгээс илүүгүй).
 , өөрөөр хэлбэл
, өөрөөр хэлбэл  . Энэ тэгш бус байдлын бүх шийдлийг олж авахын тулд энэ интервалын төгсгөлд нэмэхэд хангалттай
. Энэ тэгш бус байдлын бүх шийдлийг олж авахын тулд энэ интервалын төгсгөлд нэмэхэд хангалттай  , Хаана
, Хаана  , өөрөөр хэлбэл
, өөрөөр хэлбэл  ,
,
 .
утгууд гэдгийг анхаарна уу
.
утгууд гэдгийг анхаарна уу  Тэгээд
Тэгээд  тэгшитгэлийн үндэс юм
тэгшитгэлийн үндэс юм  ,
,
 ;
;
 .
.
 ,
,  .
.
 :
:
 Тэгээд
Тэгээд  .
.
 . Бид эдгээр цэгүүдийн абсциссуудыг олдог.
. Бид эдгээр цэгүүдийн абсциссуудыг олдог.
 Тэгээд
Тэгээд  (Зураг 2).
(Зураг 2).
 ;
;  . Энэ хооронд
. Энэ хооронд  график цэгүүд
график цэгүүд  график цэгүүдийн доор
график цэгүүдийн доор  . Тэгээд хэзээ
. Тэгээд хэзээ  функцийн утга ижил байна. Тийм ч учраас
функцийн утга ижил байна. Тийм ч учраас  цагт
цагт  .
.
 .
.
 .
.

 (Зураг 3)
(Зураг 3)

 ,
,  .
.

 ,
, 
 ,
,  .
.
 ,
, 
 .
.
 энгийн өөрчлөлтүүдийн дараа бид олж авдаг
энгийн өөрчлөлтүүдийн дараа бид олж авдаг ,
,
 ,
,
 .
.

 , тус тус
, тус тус  . Дараа нь Зураг дээрээс. 4 дагадаг
. Дараа нь Зураг дээрээс. 4 дагадаг  , Хаана
, Хаана  .
.

 ,
,  .
.
 ,
,  .
.
 .
.
 .
.
 : . Нэгж тойрог дээрх бүх цэгүүдийг тэмдэглэе (Зураг 6):
: . Нэгж тойрог дээрх бүх цэгүүдийг тэмдэглэе (Зураг 6):
 ,
,  ;
;  ,
,  ;
;  ,
,  .
.
 ,
,
 ;
;
 ,
,  ;
;
 ,
,  ;
;
 ,
,  ;
;
 . ЦувралX
2
оноо өгдөг
. ЦувралX
2
оноо өгдөг  . ЦувралаасX
3
Бид хоёр оноо авдаг
. ЦувралаасX
3
Бид хоёр оноо авдаг  . Эцэст нь цувралX
4
цэгүүдийг төлөөлөх болно
. Эцэст нь цувралX
4
цэгүүдийг төлөөлөх болно  . Эдгээр бүх цэгүүдийг нэгж тойрог дээр зурж, тэдгээрийн үржвэрийг тус бүрийн хажууд хаалтанд оруулъя.
. Эдгээр бүх цэгүүдийг нэгж тойрог дээр зурж, тэдгээрийн үржвэрийг тус бүрийн хажууд хаалтанд оруулъя. тэнцүү байх болно. Тэмдэгт дээр үндэслэн тооцоо хийцгээе.
тэнцүү байх болно. Тэмдэгт дээр үндэслэн тооцоо хийцгээе.
 цацрагтайӨө,
нэгж тойргийн гадна. (Туслах цацраг гэдгийг анхаарна ууТУХАЙ
А
Үүнийг зураг дээр дүрслэх шаардлагагүй. ЦэгА
ойролцоогоор сонгосон.)
цацрагтайӨө,
нэгж тойргийн гадна. (Туслах цацраг гэдгийг анхаарна ууТУХАЙ
А
Үүнийг зураг дээр дүрслэх шаардлагагүй. ЦэгА
ойролцоогоор сонгосон.) Манай шугам нэг хэсгээс нөгөө рүү шилждэг: хэрэв энэ нь нэгж тойргийн гадна байсан бол түүний дотор ордог. Зорилгодоо ойртож байна
Манай шугам нэг хэсгээс нөгөө рүү шилждэг: хэрэв энэ нь нэгж тойргийн гадна байсан бол түүний дотор ордог. Зорилгодоо ойртож байна  , шугам нь дотоод бүс рүү буцаж ирдэг, учир нь энэ цэгийн олон талт тэгш байдаг. Яг л цэг дээр
, шугам нь дотоод бүс рүү буцаж ирдэг, учир нь энэ цэгийн олон талт тэгш байдаг. Яг л цэг дээр  (тэгш олон талт) шугамыг гаднах бүс рүү эргүүлэх хэрэгтэй. Тиймээс бид Зураг дээр үзүүлсэн тодорхой зургийг зурсан. 7. Энэ нь нэгжийн тойрог дээр хүссэн хэсгүүдийг тодруулахад тусална. Тэд "+" тэмдгээр тэмдэглэгдсэн байдаг.
(тэгш олон талт) шугамыг гаднах бүс рүү эргүүлэх хэрэгтэй. Тиймээс бид Зураг дээр үзүүлсэн тодорхой зургийг зурсан. 7. Энэ нь нэгжийн тойрог дээр хүссэн хэсгүүдийг тодруулахад тусална. Тэд "+" тэмдгээр тэмдэглэгдсэн байдаг.
 ,
,
 ,
,  ,
,
 ,
синус ба косинусын функцүүдийн шинж чанарыг ашиглах;
,
синус ба косинусын функцүүдийн шинж чанарыг ашиглах; , Хэрэв
, Хэрэв , Хэрэв
, Хэрэв  тэнцүү байна:
тэнцүү байна: 
 , Хэрэв:
, Хэрэв:
 ,
б)
,
б)  ,
V)
,
V) 

 ,
,  ,
,  ,
,  .
.
 .
Бэлтгэл үе шатанд олж авсан мэдлэг, ур чадвараа ашиглан оюутнууд санал болгож буй тэгш бус байдлыг хэлбэрт оруулна
.
Бэлтгэл үе шатанд олж авсан мэдлэг, ур чадвараа ашиглан оюутнууд санал болгож буй тэгш бус байдлыг хэлбэрт оруулна  , гэхдээ үүссэн тэгш бус байдлын цогц шийдлүүдийг олоход хэцүү байж магадгүй, учир нь Зөвхөн синус функцийн шинж чанарыг ашиглан үүнийг шийдэх боломжгүй юм. Тохиромжтой дүрслэл (тэгшитгэлийг графикаар шийдэх эсвэл нэгж тойрог ашиглан) хийх замаар энэ хүндрэлээс зайлсхийх боломжтой.
, гэхдээ үүссэн тэгш бус байдлын цогц шийдлүүдийг олоход хэцүү байж магадгүй, учир нь Зөвхөн синус функцийн шинж чанарыг ашиглан үүнийг шийдэх боломжгүй юм. Тохиромжтой дүрслэл (тэгшитгэлийг графикаар шийдэх эсвэл нэгж тойрог ашиглан) хийх замаар энэ хүндрэлээс зайлсхийх боломжтой. .
.
 түүгээр х тэнхлэгтэй параллель шулуун шугам татна. Энэ шугам нь нэгж тойргийг хоёр цэгээр огтолно. Эдгээр цэг бүр нь синус нь тэнцүү тоонуудыг илэрхийлдэг
түүгээр х тэнхлэгтэй параллель шулуун шугам татна. Энэ шугам нь нэгж тойргийг хоёр цэгээр огтолно. Эдгээр цэг бүр нь синус нь тэнцүү тоонуудыг илэрхийлдэг  .
.
 . Мэдээжийн хэрэг, энэ нум нь зурсан шулуун шугамын дээгүүр байрладаг.
. Мэдээжийн хэрэг, энэ нум нь зурсан шулуун шугамын дээгүүр байрладаг.
 .
.
 .
.
 тэгш бус байдал үнэн байх тоонуудыг ханга
тэгш бус байдал үнэн байх тоонуудыг ханга  . Бид синусын функцийн ижил үе дээр байрлах тоонуудын тэгш бус байдлыг шийдсэн. Тиймээс тэгш бус байдлын бүх шийдлийг хэлбэрээр бичиж болно
. Бид синусын функцийн ижил үе дээр байрлах тоонуудын тэгш бус байдлыг шийдсэн. Тиймээс тэгш бус байдлын бүх шийдлийг хэлбэрээр бичиж болно ![]()
 хэлбэрээр бичиж болно
хэлбэрээр бичиж болно  ,
,  .
.

 Тэгээд
Тэгээд  , үүнийг өгсөн
, үүнийг өгсөн  .
.

 болон түүний шийдвэр
болон түүний шийдвэр  ,
,  ,
,  , томьёо ашиглан олсон
, томьёо ашиглан олсон  ,
,  ,
,  .
.
 графикуудын огтлолцох цэгүүдийн дараалсан гурван абцисса юм
графикуудын огтлолцох цэгүүдийн дараалсан гурван абцисса юм  Тэгээд
Тэгээд  . Мэдээжийн хэрэг, үргэлж интервал дээр байдаг
. Мэдээжийн хэрэг, үргэлж интервал дээр байдаг  тэгш бус байдал бий
тэгш бус байдал бий  , мөн интервал дээр
, мөн интервал дээр  - тэгш бус байдал
- тэгш бус байдал  . Бид эхний тохиолдлыг сонирхож байгаа бөгөөд дараа нь энэ интервалын төгсгөлд синусын үеийн олон тооны тоог нэмснээр тэгш бус байдлын шийдлийг олж авна.
. Бид эхний тохиолдлыг сонирхож байгаа бөгөөд дараа нь энэ интервалын төгсгөлд синусын үеийн олон тооны тоог нэмснээр тэгш бус байдлын шийдлийг олж авна.  хэлбэрээр:
хэлбэрээр:  ,
,  .
.

 , та харгалзах тэгшитгэлийг үүсгэж, шийдвэрлэх хэрэгтэй. Үүссэн томъёоноос үндсийг ол
, та харгалзах тэгшитгэлийг үүсгэж, шийдвэрлэх хэрэгтэй. Үүссэн томъёоноос үндсийг ол  Тэгээд
Тэгээд  , тэгш бус байдлын хариултыг дараах хэлбэрээр бичнэ үү. ,
, тэгш бус байдлын хариултыг дараах хэлбэрээр бичнэ үү. ,  .
.


![]()
![]()
 , нөхцөлийг хангаж байна
, нөхцөлийг хангаж байна  ;
;
 , нөхцөлийг хангаж байна
, нөхцөлийг хангаж байна  .
.
 ;
;
 ;
;
 .
.
 ;
;
 .
.
 ;
;
 ;
;
 ;
;
 ;
;

 , ХаанаП
(
x
)
ТэгээдQ
(
x
)
– рационал тэгш бус байдлыг шийдвэрлэхтэй адил рационал тригонометрийн функцууд (синус, косинус, тангенс ба котангенсууд нь рациональ байдлаар орно). Тооны шулуун дээрх интервалын аргыг ашиглан рационал тэгш бус байдлыг шийдвэрлэхэд тохиромжтой. Рационал тригонометрийн тэгш бус байдлыг шийдвэрлэх аналог нь тригонометрийн тойрог дахь секторуудын арга юм.синкс
Тэгээдcosx
(
, ХаанаП
(
x
)
ТэгээдQ
(
x
)
– рационал тэгш бус байдлыг шийдвэрлэхтэй адил рационал тригонометрийн функцууд (синус, косинус, тангенс ба котангенсууд нь рациональ байдлаар орно). Тооны шулуун дээрх интервалын аргыг ашиглан рационал тэгш бус байдлыг шийдвэрлэхэд тохиромжтой. Рационал тригонометрийн тэгш бус байдлыг шийдвэрлэх аналог нь тригонометрийн тойрог дахь секторуудын арга юм.синкс
Тэгээдcosx
( ) эсвэл тригонометрийн хагас тойрогtgx
Тэгээдctgx
(
) эсвэл тригонометрийн хагас тойрогtgx
Тэгээдctgx
(
 ).
).
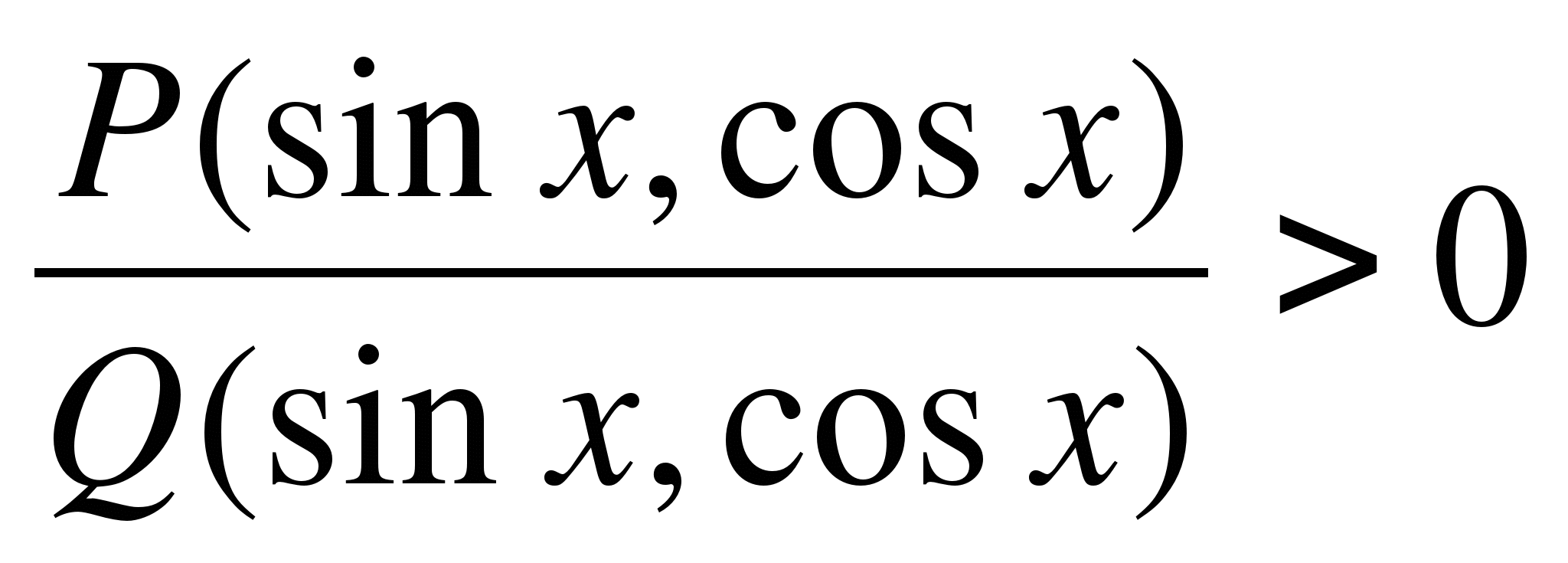
 тооны тэнхлэг дээрх цэгтэй тохирч байна
тооны тэнхлэг дээрх цэгтэй тохирч байна  , мөн энэ цэгээр дамжин өнгөрөх үед
, мөн энэ цэгээр дамжин өнгөрөх үед  тэмдгийг өөрчилдөг. Салбарын аргад маягтын хүчин зүйл бүр
тэмдгийг өөрчилдөг. Салбарын аргад маягтын хүчин зүйл бүр  , Хаана
, Хаана  - функцүүдийн нэгсинкс
эсвэлcosx
Тэгээд
- функцүүдийн нэгсинкс
эсвэлcosx
Тэгээд  , тригонометрийн тойрогт тохирох хоёр өнцөг байна
, тригонометрийн тойрогт тохирох хоёр өнцөг байна  Тэгээд
Тэгээд 
 , энэ нь тойргийг хоёр секторт хуваадаг. Хажуугаар нь өнгөрөхдөө
, энэ нь тойргийг хоёр секторт хуваадаг. Хажуугаар нь өнгөрөхдөө  Тэгээд
Тэгээд  функц
функц  тэмдгийг өөрчилдөг.
тэмдгийг өөрчилдөг. Тэгээд
Тэгээд  , Хаана
, Хаана  , бүх утгын тэмдгийг хадгална
, бүх утгын тэмдгийг хадгална  . Тоолуур ба хуваагчийн ийм хүчин зүйлийг өөрчлөх замаар устгана (хэрэв
. Тоолуур ба хуваагчийн ийм хүчин зүйлийг өөрчлөх замаар устгана (хэрэв  ) ийм татгалзах бүрт тэгш бус байдлын тэмдэг эсрэгээр өөрчлөгдөнө.
) ийм татгалзах бүрт тэгш бус байдлын тэмдэг эсрэгээр өөрчлөгдөнө. Тэгээд
Тэгээд  бас хаядаг. Түүнээс гадна, хэрэв эдгээр нь хуваагчийн хүчин зүйлүүд бол тэгш бус байдлын эквивалент системд хэлбэрийн тэгш бус байдлыг нэмнэ.
бас хаядаг. Түүнээс гадна, хэрэв эдгээр нь хуваагчийн хүчин зүйлүүд бол тэгш бус байдлын эквивалент системд хэлбэрийн тэгш бус байдлыг нэмнэ.  Тэгээд
Тэгээд  . Хэрэв эдгээр нь тоологчийн хүчин зүйлүүд юм бол хязгаарлалтын эквивалент системд тэдгээр нь тэгш бус байдалд тохирно.
. Хэрэв эдгээр нь тоологчийн хүчин зүйлүүд юм бол хязгаарлалтын эквивалент системд тэдгээр нь тэгш бус байдалд тохирно.  Тэгээд
Тэгээд  хатуу анхны тэгш бус байдлын хувьд, мөн тэгш байдал
хатуу анхны тэгш бус байдлын хувьд, мөн тэгш байдал  Тэгээд
Тэгээд  хатуу бус анхны тэгш бус байдлын хувьд. Үржүүлэгчийг хаях үед
хатуу бус анхны тэгш бус байдлын хувьд. Үржүүлэгчийг хаях үед  эсвэл
эсвэл  тэгш бус байдлын тэмдэг урвуу байна.
тэгш бус байдлын тэмдэг урвуу байна. , б)
, б)  .
Бидэнд b) функц байна. Бидэнд байгаа тэгш бус байдлыг шийдэж,
.
Бидэнд b) функц байна. Бидэнд байгаа тэгш бус байдлыг шийдэж,


 ,
,  .
.














 шийдэл:цагт
шийдэл:цагт





