For at skrive et rationelt tal m/n som en decimalbrøk skal du dividere tælleren med nævneren. I dette tilfælde skrives kvotienten som en endelig eller uendelig decimalbrøk.

Skriv dette tal som en decimalbrøk.

Løsning. Opdel tælleren for hver brøk i en kolonne med dens nævner: EN) divider 6 med 25; b) divider 2 med 3; V) divider 1 med 2, og tilføj derefter den resulterende brøk til en - den heltallige del af dette blandede tal.

Ureducerbar almindelige brøker, hvis nævnere ikke indeholder andre primfaktorer end 2 Og 5 , skrives som en sidste decimalbrøk.

I eksempel 1 i tilfælde af EN) nævner 25=5·5; i tilfælde af V) nævneren er 2, så vi fik finalen decimaler 0,24 og 1,5. I tilfælde af b) nævneren er 3, så resultatet kan ikke skrives som en endelig decimal.

Er det muligt uden lang division at konvertere en sådan almindelig brøk til en decimalbrøk, hvis nævner ikke indeholder andre divisorer end 2 og 5? Lad os finde ud af det! Hvilken brøk kaldes en decimal og skrives uden en brøklinje? Svar: brøk med nævner 10; 100; 1000 osv. Og hvert af disse tal er et produkt lige antal toere og femmere. Faktisk: 10=2 ·5; 100=2 ·5 ·2 ·5; 1000=2 ·5 ·2 ·5 ·2 ·5 osv.

Som følge heraf skal nævneren for en irreducerbar almindelig brøk repræsenteres som produktet af "toere" og "femmer" og derefter ganges med 2 og (eller) 5, så "toere" og "fem" bliver lige store. Så vil nævneren af ​​brøken være lig med 10 eller 100 eller 1000 osv. For at sikre, at værdien af ​​brøken ikke ændres, multiplicerer vi brøkens tæller med det samme tal, som vi gangede nævneren med.

Udtryk følgende almindelige brøker som decimaler:

Løsning. Hver af disse fraktioner er irreducerbare. Lad os indregne nævneren for hver brøk i primfaktorer.

20=2·2·5. Konklusion: et "A" mangler.

8=2·2·2. Konklusion: tre "A" mangler.

25=5·5. Konklusion: to "toere" mangler.

Kommentar. I praksis bruger de ofte ikke faktorisering af nævneren, men stiller blot spørgsmålet: hvor meget skal nævneren ganges med, så resultatet bliver ét med nuller (10 eller 100 eller 1000 osv.). Og så ganges tælleren med det samme tal.

Så i tilfælde af EN)(eksempel 2) fra tallet 20 kan du få 100 ved at gange med 5, derfor skal du gange tælleren og nævneren med 5.

I tilfælde af b)(eksempel 2) fra tallet 8 opnås tallet 100 ikke, men tallet 1000 opnås ved at gange med 125. Både brøkens tæller (3) og nævner (8) ganges med 125.

I tilfælde af V)(eksempel 2) fra 25 får man 100, hvis man ganger med 4. Det betyder, at tælleren 8 skal ganges med 4.

En uendelig decimalbrøk, hvor et eller flere cifre uvægerligt gentages i samme rækkefølge kaldes periodisk som en decimal. Sættet af gentagne cifre kaldes perioden for denne brøk. For kortheds skyld skrives perioden for en brøk én gang, omgivet af parentes.

I tilfælde af b)(eksempel 1) der er kun ét gentaget ciffer og er lig med 6. Derfor vil vores resultat 0,66... skrives således: 0,(6) . De læste: nul point, seks i punktum.

Hvis der er et eller flere ikke-gentagende cifre mellem decimaltegnet og det første punktum, så kaldes en sådan periodisk brøk en blandet periodisk brøk.

En irreducerbar fællesbrøk, hvis nævner er sammen med andre multiplikatorer indeholder en multiplikator 2 eller 5 , vender sig til blandet periodisk fraktion.

Skriv tallene som en decimalbrøk:

Ethvert rationelt tal kan skrives som en uendelig periodisk decimalbrøk.

Skriv tallene som en uendelig periodisk brøk.

Periodisk fraktion

en uendelig decimalbrøk, hvor der, startende fra et bestemt punkt, kun er en periodisk gentaget bestemt gruppe af cifre. For eksempel, 1.3181818...; Kort fortalt skrives denne brøk således: 1,3(18), det vil sige, at de sætter punktum i parentes (og siger: “18 i perioden”). P. kaldes ren, hvis punktum begynder umiddelbart efter decimalkommaet, for eksempel 2(71) = 2,7171..., og blandet, hvis der efter decimalpunktet er tal foran punktum, for eksempel 1,3(18). Decimalbrøkernes rolle i aritmetikken skyldes, at når rationelle tal, det vil sige almindelige (simple) brøker, er repræsenteret ved decimalbrøker, opnås altid enten endelige eller periodiske brøker. Mere præcist: en endelig decimalbrøk opnås, når nævneren af ​​en irreducerbar simpel brøk ikke indeholder andre primfaktorer end 2 og 5; i alle andre tilfælde er resultatet en P.-brøk, og desuden er den ren, hvis nævneren for en given irreducerbar brøk slet ikke indeholder faktorerne 2 og 5, og blandet, hvis mindst én af disse faktorer er indeholdt i nævneren. Enhver P.D. kan konverteres til simpel brøk(det vil sige, at det er lig med et eller andet rationelt tal). En ren brøk er lig med en simpel brøk, hvis tæller er perioden, og nævneren er repræsenteret ved tallet 9, skrevet lige så mange gange, som der er cifre i perioden; Når man konverterer en blandet brøk til en simpel brøk, er tælleren forskellen mellem tallet repræsenteret af tallene forud for den anden periode og tallet repræsenteret af tallene forud for den første periode; For at sammensætte nævneren skal du skrive tallet 9 lige så mange gange, som der er tal i perioden, og tilføje lige så mange nuller til højre, som der er tal før perioden. Disse regler antager, at den givne P. er korrekt, dvs. den indeholder ikke hele enheder; ellers tages der særligt hensyn til hele delen.

Reglerne for at bestemme længden af ​​perioden for en brøk svarende til en given almindelig brøk er også kendt. For eksempel for en brøkdel a/p, Hvor r - primtal og 1 ≤ -en ≤ p- 1, er periodelængde en divisor r - 1. Så for kendte tilnærmelser til et tal (se Pi) 22/7 og 355/113 perioder er lig med henholdsvis 6 og 112.

Store sovjetiske encyklopædi. - M.: Sovjetisk Encyklopædi. 1969-1978 .

Synonymer:

Se, hvad "Periodisk brøk" er i andre ordbøger:

En uendelig decimalbrøk, hvor f.eks. med udgangspunkt i et bestemt punkt en bestemt gruppe af cifre (punktum) periodisk gentages. 0,373737... ren periodisk fraktion eller 0,253737... blandet periodisk fraktion... Stor Encyklopædisk ordbog

Brøk, uendelig brøkdel Ordbog over russiske synonymer. periodisk brøk substantiv, antal synonymer: 2 uendelig brøk (2) ... Ordbog over synonymer

En decimalbrøk, hvor en række cifre gentages i samme rækkefølge. For eksempel er 0,135135135... en p.d. hvis periode er 135, og som er lig med den simple brøk 135/999 = 5/37. Ordbog over fremmede ord inkluderet i det russiske sprog. Pavlenkov F... Ordbog over fremmede ord i det russiske sprog

En decimal er en brøk med nævneren 10n, hvor n er et naturligt tal. Har speciel form indgange: en heltalsdel i decimaltalsystemet, derefter et komma og derefter en brøkdel i decimaltalsystemet, og antallet af cifre i brøkdelen ... Wikipedia

En uendelig decimalbrøk, hvor en bestemt gruppe af cifre (punktum) med udgangspunkt i et bestemt punkt gentages periodisk; for eksempel 0,373737... ren periodisk fraktion eller 0,253737... blandet periodisk fraktion. * * * PERIODISK … … Encyklopædisk ordbog

En endeløs decimalbrøk, hvor definitionen med udgangspunkt fra et bestemt sted gentages periodisk. gruppe af cifre (punktum); for eksempel 0,373737... ren P. d. eller 0,253737... blandet P. d. Naturvidenskab. Encyklopædisk ordbog

Se del... Ordbog over russiske synonymer og lignende udtryk. under. udg. N. Abramova, M.: Russian Dictionaries, 1999. brøk trifli, del; dunst, bold, mel, buckshot; brøktal Ordbog over russiske synonymer... Ordbog over synonymer

periodisk decimal- - [L.G. Sumenko. Engelsk-russisk ordbog om informationsteknologi. M.: Statsvirksomhed TsNIIS, 2003.] Emner informationsteknologi generelt EN cirkulerende decimaltilbagevendende decimalperioder decimalperiodisk decimalperiodisk decimal ... Teknisk oversættervejledning

Hvis et eller andet heltal a divideres med et andet heltal b, dvs. der søges efter et tal x, der opfylder betingelsen bx = a, så kan der opstå to tilfælde: enten er der i rækken af ​​heltal et tal x, der opfylder denne betingelse, eller det viser sig, … … Encyklopædisk ordbog F.A. Brockhaus og I.A. Ephron

En brøk, hvis nævner er en heltalspotens på 10. Brøker skrives uden nævner, der adskiller lige så mange cifre i tælleren til højre med et komma, som der er nuller i nævneren. For eksempel, i en sådan optegnelse, delen til venstre... ... Store sovjetiske encyklopædi

Uendelige decimaler

Decimaler efter decimaltegnet kan indeholde et uendeligt antal cifre.

Uendelige decimaler- det er decimalbrøker, som indeholder et uendeligt antal cifre.

En uendelig decimalbrøk er næsten umulig at skrive helt ned, så når de skrives, er de begrænset til kun et bestemt endeligt antal cifre efter decimalkommaet, hvorefter de sætter en ellipse, som angiver en uendeligt fortsættende talfølge.

Eksempel 1

For eksempel $0,443340831\dots ; 3.1415935432\prikker ; 135.126730405\dots ; 4.33333333333\prikker ; 676.68349349\dots$.

Lad os se på de sidste to uendelige decimaler. I brøken $4,333333333333\dots$ gentages tallet $3$ i det uendelige, og i brøken $676,68349349\dots$ gentages cifrene $3$, $4$ og $9$ fra tredje decimal. Sådanne uendelige decimalbrøker kaldes periodiske.

Periodiske decimaler

Periodiske decimaler(eller periodiske brøker) er uendelige decimalbrøker, i hvis optagelse et eller andet tal eller gruppe af tal, kaldet brøkens periode, gentages uendeligt fra en bestemt decimal).

Eksempel 2

For eksempel er perioden for den periodiske brøk $4.33333333333\dots$ cifferet $3$, og perioden for brøken $676.68349349\dots$ er gruppen af ​​cifre $349$.

For kortheds skyld ved at skrive uendelige periodiske decimalbrøker, er det sædvanligt at skrive punktum én gang, omsluttende det i parentes. For eksempel skrives den periodiske brøk $4,333333333333\dots$ $4,(3)$, og den periodiske brøk $676,68349349\dots$ skrives $676,68(349)$.

Uendelige periodiske decimalbrøker opnås ved at konvertere almindelige brøker, hvis nævnere indeholder andre primfaktorer end $2$ og $5$ til decimalbrøker.

Enhver endelig decimalbrøk (og heltal) kan skrives som en periodisk brøk ved at tilføje et uendeligt antal cifre $0$ til højre.

Eksempel 3

For eksempel kunne den endelige decimal $45,12$ skrives som en periodisk brøk som $45,12(0)$, og heltallet $(74)$ som en uendelig periodisk decimal ville være $74(0)$.

I tilfælde af periodiske brøker, der har en periode på 9, skal du bruge en overgang til en anden notation af en periodisk brøk med en periode på $0$. Kun til dette formål erstattes periode 9 med periode $0$, og værdien af ​​det næsthøjeste ciffer øges med $1$.

Eksempel 4

For eksempel kan den periodiske brøk $7,45(9)$ erstattes af den periodiske brøk $7,46(0)$ eller den tilsvarende decimalbrøk $7,46$.

Uendelige decimale periodiske brøker er repræsenteret rationelle tal. Med andre ord kan enhver periodisk brøk omdannes til en almindelig brøk, og enhver almindelig brøk kan repræsenteres som en periodisk brøk.

Konvertering af brøker til endelige og uendelige periodiske decimaler

Ikke kun almindelige brøker med nævnere $10, 100, \dots$ kan konverteres til en decimalbrøk.

I nogle tilfælde kan den oprindelige fællesbrøk let reduceres til en nævner på $10$, $100$ eller $1\000$, hvorefter den resulterende brøk kan repræsenteres som en decimalbrøk.

Eksempel 5

For at konvertere brøken $\frac(3)(5)$ til en brøk med nævneren $10$, skal du gange brøkens tæller og nævner med $2$, hvorefter vi får $\frac(6)( 10)$, hvilket ikke er svært at oversætte til decimalbrøken $0,6$.

I andre tilfælde bruges en anden metode til at konvertere en fælles brøk til en decimal):

tælleren skal erstattes med en decimalbrøk med et vilkårligt antal nuller efter decimaltegnet;

divider brøkens tæller med nævneren (divisionen udføres som en division af naturlige tal i en kolonne, og i kvotienten placeres et decimaltegn efter slutningen af ​​divisionen af ​​hele udbyttedelen).

Eksempel 6

Konverter brøken $\frac(621)(4)$ til en decimal.

Løsning.

Lad os repræsentere tallet $621$ i tælleren som en decimalbrøk. For at gøre dette skal du tilføje et decimaltegn og, for det første, to nuller efter det. Så kan du eventuelt tilføje flere nuller. Så vi modtog $621,00$.

Lad os dele tallet $621.00$ med $4$ i en kolonne:

Figur 1.

Divisionen nåede decimalkommaet i udbyttet, og resten var ikke nul. I dette tilfælde placeres et decimaltegn i kvotienten, og divisionen fortsætter i en kolonne, uanset kommaerne:

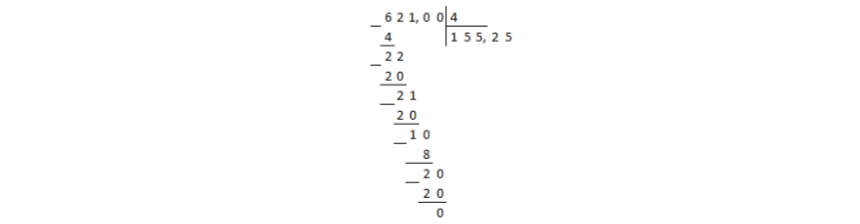
Figur 2.

Resten er nul, hvilket betyder, at divisionen er slut.

Svar: $155,25$.

Det er muligt, at når man dividerer tælleren og nævneren af ​​en almindelig brøk, resulterer resten ikke i $0$. I dette tilfælde kan opdelingen fortsættes på ubestemt tid. Startende fra et bestemt punkt gentages resten fra division periodisk, hvilket betyder, at tallene i kvotienten også gentages. Ud fra dette kan vi konkludere, at denne almindelige brøk vil blive omdannet til en uendelig periodisk decimalbrøk.

Eksempel 7

Konverter brøken $\frac(19)(44)$ til en decimal.

Løsning.)

For at konvertere en fælles brøk til en decimal skal du udføre lang division:

Figur 3.

Ved division gentages resten $8$ og $36$, og i kvotienten gentages også tallene $1$ og $8$. Så den oprindelige almindelige brøk $\frac(19)(44)$ blev konverteret til en periodisk brøk $\frac(19)(44)=0,43181818\dots =0,43(18)$.

Svar: $0,43(18)$.

Generel konklusion om konvertering af almindelige brøker til decimaler:

hvis nævneren kan dekomponeres i primfaktorer, blandt hvilke kun tallene $2$ og $5$ vil være til stede, så kan en sådan brøk konverteres til en endelig decimalbrøk;

hvis nævnerens udvidelse ud over tallene $2$ og $5$ indeholder andre primtal, så konverteres en sådan brøk til en uendelig decimal periodisk brøk.

At hvis de kender serieteorien, så kan der ikke indføres metamatiske begreber uden den. Desuden tror disse mennesker, at enhver, der ikke bruger det bredt, er uvidende. Lad os overlade disse menneskers synspunkter til deres samvittighed. Lad os bedre forstå, hvad en uendelig periodisk brøk er, og hvordan vi, uuddannede mennesker, der ikke kender nogen grænser, bør håndtere det.

Lad os dividere 237 med 5. Nej, du behøver ikke at starte lommeregneren. Lad os bedre huske gymnasiet (eller endda folkeskolen?) og simpelthen opdele det i en kolonne:

Nå, huskede du? Så kan du komme i gang.

Begrebet "brøk" i matematik har to betydninger:

1. Ikke-heltal tal.
2. Ikke-heltalsform.

Der er to typer brøker - i betydningen to former for skrivning af ikke-heltal:

1. Simpelt (eller lodret) brøker, såsom 1/2 eller 237/5.
2. Decimalbrøker, såsom 0,5 eller 47,4.

Bemærk, at selve brugen af ​​en brøknotation generelt ikke betyder, at det der skrives er et brøktal, for eksempel 3/3 eller 7,0 - ikke brøker i ordets første betydning, men i den anden, selvfølgelig , brøker.

I matematik er decimaltælling generelt altid blevet accepteret, og derfor er decimalbrøker mere bekvemme end simple, det vil sige en brøk med en decimalnævner (Vladimir Dal. Ordbog lever stort russisk sprog. "Ti").

Og hvis ja, så vil jeg gøre hver lodret brøk til en decimal ("vandret"). Og for at gøre dette skal du blot dividere tælleren med nævneren. Lad os for eksempel tage brøken 1/3 og prøve at lave en decimal ud af den.

Selv en fuldstændig uuddannet person vil bemærke: uanset hvor lang tid det tager, vil det ikke adskilles: trillinger vil fortsætte med at dukke op i det uendelige. Så lad os skrive det ned: 0,33... Vi mener "det tal, der opnås, når du dividerer 1 med 3," eller kort sagt "en tredjedel." Naturligvis er en tredjedel en brøk i ordets første betydning, og "1/3" og "0,33..." er brøker i ordets anden betydning, dvs. tilmeldingsformularer et tal, der er placeret på tallinjen i en sådan afstand fra nul, at hvis du lægger det til side tre gange, får du en.

Lad os nu prøve at dividere 5 med 6:

Lad os skrive det ned igen: 0,833... Vi mener "det tal, du får, når du dividerer 5 med 6," eller kort sagt "fem sjettedele." Men der opstår forvirring her: betyder det 0,83333 (og så gentages tripletterne) eller 0,833833 (og så gentages 833). Derfor passer notation med ellipse ikke os: det er ikke klart, hvor den gentagne del begynder (det kaldes "periode"). Derfor vil vi sætte punktum i parentes, således: 0,(3); 0,8(3).

0,(3) ikke let lig med en tredjedel, altså Der er en tredjedel, fordi vi specielt opfandt denne notation til at repræsentere dette tal som en decimalbrøk.

Denne post kaldes uendelig periodisk brøk, eller blot en periodisk brøk.

Hver gang vi dividerer et tal med et andet, hvis vi ikke får en endelig brøk, får vi en uendelig periodisk brøk, det vil sige, en dag vil talsekvenserne helt sikkert begynde at gentage sig. Hvorfor det er sådan, kan forstås rent spekulativt ved at se nøje på kolonneopdelingsalgoritmen:

På de steder, der er markeret med flueben, kan du ikke få resultater hele tiden forskellige par tal (fordi der i princippet er et begrænset antal af sådanne par). Og så snart et sådant par dukker op der, som allerede eksisterede, vil forskellen også være den samme - og så vil hele processen begynde at gentage sig selv. Der er ingen grund til at kontrollere dette, for det er ret indlysende, at hvis du gentager de samme handlinger, vil resultaterne være de samme.

Nu forstår vi det godt essens periodisk brøk, lad os prøve at gange en tredjedel med tre. Ja, selvfølgelig får du en, men lad os skrive denne brøk i decimalform og gange den i en kolonne (tvetydighed opstår ikke her på grund af ellipsen, da alle tallene efter decimaltegnet er de samme):

Og igen bemærker vi, at ni, ni og nie vil dukke op efter decimaltegnet hele tiden. Det vil sige, ved at bruge den omvendte parentesnotation får vi 0,(9). Da vi ved, at produktet af en tredjedel og tre er en, så er 0.(9) sådan en fancy måde at skrive en på. Det er dog uhensigtsmæssigt at bruge denne form for optagelse, fordi en enhed kan skrives perfekt uden at bruge et punktum, som denne: 1.

Som du kan se, er 0,(9) et af de tilfælde, hvor hele tallet er skrevet i brøkform, som 3/3 eller 7,0. Det vil sige, at 0,(9) kun er en brøk i ordets anden betydning, men ikke i den første.

Så uden nogen begrænsninger eller serier fandt vi ud af, hvad 0.(9) er, og hvordan vi skal håndtere det.

Men lad os stadig huske, at vi faktisk er smarte og studerede analyser. Det er faktisk svært at benægte, at:

Men måske vil ingen argumentere med det faktum, at:

Alt dette er selvfølgelig sandt. Faktisk er 0,(9) både summen af ​​den reducerede række og den dobbelte sinus af den angivne vinkel og den naturlige logaritme af Euler-tallet.

Men hverken det ene, det andet eller det tredje er en definition.

At sige, at 0,(9) er summen af ​​den uendelige række 9/(10 n), med n lig med én, er det samme som at sige, at sinus er summen af ​​den uendelige Taylor-række:

Denne helt rigtigt, og dette er den vigtigste kendsgerning for beregningsmatematik, men det er ikke en definition, og vigtigst af alt, det bringer ikke en person nærmere forståelse i det væsentlige bihule Essensen af ​​sinus af en bestemt vinkel er, at den bare alt forholdet mellem benet modsat vinklen og hypotenusen.

Så en periodisk brøk er bare alt en decimalbrøk, der opnås når når man dividerer med en kolonne det samme sæt tal vil blive gentaget. Der er ingen spor af analyse her.

Og det er her spørgsmålet opstår: hvor kommer det fra? overhovedet tog vi tallet 0,(9)? Hvad dividerer vi med med en kolonne for at få det? Faktisk er der ingen tal, så når de er opdelt i en kolonne, ville vi have uendeligt optrædende niere. Men det lykkedes os at få dette tal ved at gange 0,(3) med 3 med en kolonne? Ikke rigtig. Når alt kommer til alt, skal du gange fra højre til venstre for korrekt at tage højde for overførsler af cifre, og vi gjorde dette fra venstre mod højre, idet vi snedigt udnyttede det faktum, at overførsler alligevel ikke forekommer nogen steder. Derfor afhænger lovligheden af ​​at skrive 0,(9) af, om vi anerkender lovligheden af ​​en sådan multiplikation med en kolonne eller ej.

Derfor kan vi generelt sige, at notationen 0,(9) er forkert - og til en vis grad være rigtig. Men da notationen a ,(b ) er accepteret, er det simpelthen grimt at opgive det, når b = 9; Det er bedre at beslutte, hvad en sådan post betyder. Så hvis vi generelt accepterer notationen 0,(9), så betyder denne notation selvfølgelig tallet et.

Det er kun tilbage at tilføje, at hvis vi f.eks. brugte det ternære talsystem, så ville vi, når vi dividerede med en kolonne på en (1 3) med tre (10 3) få 0,1 3 (læs "nul komma en tredjedel"). og når man dividerer en efter to ville være 0,(1) 3.

Så periodiciteten af ​​et brøktal er ikke en objektiv karakteristik af et brøktal, men blot bivirkning ved hjælp af et eller andet talsystem.

§ 114. Omregning af en almindelig brøk til en decimal.

At konvertere en fællesbrøk til en decimal betyder at finde en decimalbrøk, der ville være lig med den givne fællesbrøk. Når vi konverterer almindelige brøker til decimaler, vil vi støde på to tilfælde:

1) når almindelige brøker kan omregnes til decimaler nøjagtig;

2) når almindelige brøker kun kan omregnes til decimaler tilnærmelsesvis. Lad os overveje disse sager sekventielt.

1. Hvordan konverterer man en almindelig irreducerbar brøk til en decimal, eller med andre ord, hvordan erstatter man en almindelig brøk med en decimal lig med den?

I det tilfælde, hvor almindelige brøker kan være nøjagtig omregnet til decimal, er der to måder sådan behandling.

Lad os huske, hvordan man erstatter en brøk med en anden, der er lig med den første, eller hvordan man flytter fra en brøk til en anden uden at ændre værdien af ​​den første. Det gjorde vi, da vi reducerede brøker til en fællesnævner (§86). Når vi reducerer brøker til en fællesnævner, går vi frem som følger: vi finder fællesnævner for givne brøker beregner vi en ekstra faktor for hver brøk og multiplicerer derefter tælleren og nævneren for hver brøk med denne faktor.

Efter at have bemærket dette, lad os tage den irreducible brøk 3/20 og prøve at konvertere den til en decimal. Nævneren af ​​denne brøk er 20, men du skal bringe den til en anden nævner, som ville være repræsenteret af en med nuller. Vi leder efter den mindste nævner af én efterfulgt af nuller.

Første vej konvertering af en fælles brøk til en decimal er baseret på at dekomponere nævneren i primtal.

Du skal finde ud af hvilket tal du skal gange 20 med, så produktet udtrykkes som et efterfulgt af nuller. For at finde ud af det, skal du først huske i hvilke primfaktorer tallene repræsenteret af en og nuller er dekomponeret. Disse er nedbrydningerne:

10 = 2 5,
100 = 2 2 5 . 5,
1 000 = 2 2 2 5 5 5,
10 000 = 2 2 2 2 5 5 5 5.

Vi ser, at tallet repræsenteret af en med nuller kun dekomponeres i toere og femmere, og der er ingen andre faktorer i udvidelsen. Derudover er toere og femmere med i udvidelsen i samme antal. Og endelig er antallet af disse og andre faktorer separat lig med antallet af nuller efter den ene på billedet af et givet tal.

Lad os nu se, hvordan 20 dekomponeres i primfaktorer: 20 = 2 2 5. Heraf er det klart, at der i dekomponeringen af ​​tallet 20 er to toere og en femmer. Det betyder, at hvis vi lægger én fem til disse faktorer, får vi et tal repræsenteret af én med nuller. Med andre ord, for at nævneren skal have et tal repræsenteret af et med nuller i stedet for 20, skal du gange 20 med 5, og for at værdien af ​​brøken ikke ændres, skal du gange dens tæller med 5 , dvs.

For at konvertere en almindelig brøk til en decimal skal du derfor dekomponere nævneren af ​​denne almindelige brøk i primfaktorer og derefter udligne antallet af toere og femere i den, indsætte i den (og selvfølgelig i tælleren) ) de manglende faktorer i det nødvendige antal.

Lad os anvende denne konklusion på nogle brøker.

Konverter 3/50 til en decimal. Nævneren af ​​denne brøk udvides som følger:

Det betyder, at den mangler en toer. Lad os tilføje det:

Konverter 7/40 til en decimal.

Nævneren af ​​denne brøk dekomponeres som følger: 40 = 2 2 2 5, dvs. den mangler to femmere. Lad os introducere dem i tælleren og nævneren som faktorer:

Ud fra det anførte er det ikke svært at konkludere, hvilke almindelige brøker der konverteres nøjagtigt til decimaler. Det er helt indlysende, at en irreducerbar almindelig brøk, hvis nævner ikke indeholder andre primfaktorer end 2 og 5, konverteres nøjagtigt til en decimal. En decimalbrøk, som opnås ved at vende en almindelig brøk, vil have lige så mange decimaler som antallet af gange, som nævneren for den almindelige brøk efter dens reduktion inkluderer den numerisk dominerende faktor 2 eller 5.

Hvis vi tager brøken 9/40, vil den for det første blive til en decimal, fordi dens nævner inkluderer faktorerne 2 2 2 5, og for det andet vil den resulterende decimalbrøk have 3 decimaler, fordi den numerisk dominerende faktor 2 går i ekspansion tre gange. Faktisk:

Anden vej(ved at dividere tælleren med nævneren).

Antag, at du vil konvertere 3/4 til en decimalbrøk. Vi ved, at 3/4 er kvotienten af ​​3 divideret med 4. Vi kan finde denne kvotient ved at dividere 3 med 4. Lad os gøre dette:

Således er 3/4 = 0,75.

Et andet eksempel: konverter 5/8 til en decimalbrøk.

Så 5/8 = 0,625.

Så for at konvertere en brøk til en decimal skal du bare dividere brøkens tæller med dens nævner.

2. Lad os nu betragte det andet af de tilfælde, der er angivet i begyndelsen af ​​afsnittet, dvs. det tilfælde, hvor en almindelig brøk ikke kan omregnes til en nøjagtig decimal.

En almindelig irreducerbar brøk, hvis nævner indeholder andre primfaktorer end 2 og 5, kan ikke konverteres nøjagtigt til en decimal. Faktisk kan for eksempel brøken 8/15 ikke konverteres til en decimal, da dens nævner 15 er opdelt i to faktorer: 3 og 5.

Vi kan ikke eliminere det tredobbelte fra nævneren og kan ikke vælge et heltal, så produktet, efter at have ganget den givne nævner med det, udtrykkes som et efterfulgt af nuller.

I sådanne tilfælde kan vi kun tale om tilnærmelse almindelige brøker til decimaler.

Hvordan gøres dette? Dette gøres ved at dividere tælleren for en fælles brøk med nævneren, dvs. i dette tilfælde bruges den anden metode til at konvertere en fælles brøk til en decimal. Det betyder, at denne metode bruges til både præcis og omtrentlig håndtering.

Hvis en brøk konverteres nøjagtigt til en decimal, giver division en endelig decimalbrøk.

Hvis en almindelig brøk ikke konverteres til en nøjagtig decimal, giver division en uendelig decimalbrøk.

Da vi ikke kan udføre en endeløs divisionsproces, må vi stoppe division ved en decimal, det vil sige lave en omtrentlig division. Vi kan for eksempel lade være med at dividere med første decimal, det vil sige begrænse os til tiendedele; om nødvendigt kan vi stoppe ved anden decimal, opnå hundrededele osv. I disse tilfælde siger vi, at vi afrunder en uendelig decimalbrøk. Afrunding udføres med den nøjagtighed, der kræves for at løse dette problem.

§ 115. Begrebet periodisk brøk.

En evig decimalbrøk, hvor et eller flere cifre uvægerligt gentages i samme rækkefølge, kaldes en periodisk decimalbrøk. For eksempel:

0,33333333...; 1,12121212...; 3,234234234...

Et sæt gentagne numre kaldes periode denne fraktion. Perioden for den første af brøkerne skrevet ovenfor er 3, perioden for den anden brøk er 12, perioden for den tredje brøk er 234. Det betyder, at perioden kan bestå af flere cifre - et, to, tre osv. Det første sæt af gentagne cifre kaldes den første periode, den anden helheden - den anden periode osv., dvs.

Periodiske fraktioner kan være rene eller blandede. En periodisk brøk kaldes ren, hvis dens periode begynder umiddelbart efter decimalkommaet. Det betyder, at de periodiske brøker skrevet ovenfor vil være rene. Tværtimod kaldes en periodisk brøk blandet, hvis den har et eller flere ikke-gentagende cifre mellem decimaltegnet og det første punktum, for eksempel:

2,5333333...; 4,1232323232...; 0,2345345345345... 160

For at forkorte bogstavet kan du skrive periodetallene én gang i parentes og ikke sætte ellipse efter parenteserne, altså i stedet for 0,33... kan du skrive 0,(3); i stedet for 2,515151... kan du skrive 2,(51); i stedet for 0,2333... kan du skrive 0,2(3); i stedet for 0,8333... kan du skrive 0,8(3).

Periodiske brøker læses således:

0,(3) - 0 heltal, 3 i punktum.

7,2(3) - 7 heltal, 2 før perioden, 3 i perioden.

5.00(17) - 5 heltal, to nuller før perioden, 17 i perioden.

Hvordan opstår periodiske brøker? Vi har allerede set, at når man konverterer brøker til decimaler, kan der være to tilfælde.

For det første, nævneren af ​​en almindelig irreducerbar brøk indeholder ikke andre faktorer end 2 og 5; i dette tilfælde bliver den almindelige brøk en sidste decimal.

For det andet nævneren for en almindelig irreducerbar brøk indeholder alle andre primfaktorer end 2 og 5; i dette tilfælde bliver den almindelige brøk ikke til en sidste decimal. I sidstnævnte tilfælde vil et forsøg på at konvertere en brøk til en decimal ved at dividere tælleren med nævneren resultere i en uendelig brøk, der altid vil være periodisk.

For at se dette, lad os se på et eksempel. Lad os prøve at konvertere brøken 18/7 til en decimal.

Vi ved selvfølgelig på forhånd, at en brøk med en sådan nævner ikke kan omregnes til en endelig decimal, og vi taler kun om en omtrentlig omregning. Divider tælleren 18 med nævneren 7.

Vi fik otte decimaler i kvotienten. Der er ingen grund til at fortsætte opdelingen yderligere, for den ender alligevel ikke. Men heraf fremgår det, at divisionen kan fortsættes i det uendelige og dermed få nye tal i kvotienten. Disse nye tal vil opstå, fordi vi altid vil have rester; men ingen rest kan være større end divisoren, som for os er 7.

Lad os se, hvilke saldi vi havde: 4; 5; 1; 3; 2; b, dvs. det var tal mindre end 7. Dem kan der naturligvis ikke være mere end seks af, og med videre fortsættelse af divisionen skal de gentages, og efter dem vil kvotientens cifre blive gentaget. Ovenstående eksempel bekræfter denne idé: decimalerne i kvotienten er i denne rækkefølge: 571428, og derefter dukkede tallene 57 op igen. Det betyder, at den første punktum er slut, og den anden begynder.

Således, en uendelig decimalbrøk opnået ved at invertere en fællesbrøk vil altid være periodisk.

Hvis man støder på en periodisk brøkdel, når man løser et problem, tages den med den nøjagtighed, som betingelserne for problemet kræver (til tiendedelen, til hundrededelen, til tusindedelen osv.).

§ 116. Fællesaktioner med almindelige og decimalbrøker.

Når man beslutter sig forskellige opgaver Vi vil støde på tilfælde, hvor problemet involverer både almindelige og decimalbrøker.

I disse tilfælde kan du gå på forskellige måder.

1. Konverter alle brøker til decimaler. Dette er praktisk, fordi beregninger med decimalbrøker er nemmere end med almindelige brøker. f.eks.

Lad os konvertere brøkerne 3/4 og 1 1/5 til decimaler:

2. Omregn alle brøker til almindelige brøker. Dette gøres oftest i tilfælde, hvor der er almindelige brøker, der ikke bliver til endelige decimaler.

f.eks.

Lad os konvertere decimalbrøker til almindelige brøker:

3. Beregninger udføres uden at konvertere nogle brøker til andre.

Dette er især nyttigt, når eksemplet kun involverer multiplikation og division. f.eks.

Lad os omskrive eksemplet sådan her:

4. I nogle tilfælde konverter alle brøker til decimaler(selv dem, der bliver til periodiske) og find et omtrentligt resultat. f.eks.

Lad os konvertere 2/3 til en decimalbrøk og begrænse os til tusindedele.