Κατά την επίλυση ανισώσεων που περιέχουν τριγωνομετρικές συναρτήσεις, αυτές ανάγονται στις απλούστερες ανισώσεις της μορφής cos(t)>a, sint(t)=a και παρόμοιες. Και ήδη οι πιο απλές ανισότητες έχουν λυθεί. Ας δούμε διάφορα παραδείγματατρόποι επίλυσης απλών τριγωνομετρικών ανισώσεων.
Παράδειγμα 1. Λύστε την ανίσωση sin(t) > = -1/2.
Σχεδιάστε έναν κύκλο μονάδας. Εφόσον το sin(t) εξ ορισμού είναι η συντεταγμένη y, σημειώνουμε το σημείο y = -1/2 στον άξονα Oy. Τραβάμε μια ευθεία γραμμή μέσω αυτής παράλληλη με τον άξονα Ox. Στην τομή της ευθείας με τη γραφική παράσταση του μοναδιαίου κύκλου, σημειώστε τα σημεία Pt1 και Pt2. Συνδέουμε την αρχή των συντεταγμένων με τα σημεία Pt1 και Pt2 με δύο τμήματα.
Η λύση σε αυτήν την ανισότητα θα είναι όλα τα σημεία του μοναδιαίου κύκλου που βρίσκονται πάνω από αυτά τα σημεία. Με άλλα λόγια, η λύση θα είναι το τόξο l Τώρα είναι απαραίτητο να υποδείξουμε τις συνθήκες υπό τις οποίες ένα αυθαίρετο σημείο θα ανήκει στο τόξο l.
Το Pt1 βρίσκεται στο δεξιό ημικύκλιο, η τεταγμένη του είναι -1/2, τότε t1=arcsin(-1/2) = - pi/6. Για να περιγράψετε το σημείο Pt1, μπορείτε να γράψετε τον ακόλουθο τύπο:
t2 = pi - arcsin(-1/2) = 7*pi/6. Ως αποτέλεσμα, λαμβάνουμε την ακόλουθη ανισότητα για t:
Διατηρούμε τις ανισότητες. Και επειδή η ημιτονοειδής συνάρτηση είναι περιοδική, σημαίνει ότι οι λύσεις θα επαναλαμβάνονται κάθε 2*pi. Προσθέτουμε αυτή τη συνθήκη στην προκύπτουσα ανισότητα για το t και γράφουμε την απάντηση.
Απάντηση: -pi/6+2*pi*n< = t < = 7*pi/6 + 2*pi*n, при любом целом n.
Παράδειγμα 2.Επίλυση της ανισότητας κόστους(t).<1/2.
Ας σχεδιάσουμε έναν κύκλο μονάδας. Εφόσον, σύμφωνα με τον ορισμό, cos(t) είναι η συντεταγμένη x, σημειώνουμε το σημείο x = 1/2 στη γραφική παράσταση στον άξονα Ox.
Τραβάμε μια ευθεία γραμμή μέσα από αυτό το σημείο παράλληλη με τον άξονα Oy. Στην τομή της ευθείας με τη γραφική παράσταση του μοναδιαίου κύκλου, σημειώστε τα σημεία Pt1 και Pt2. Συνδέουμε την αρχή των συντεταγμένων με τα σημεία Pt1 και Pt2 με δύο τμήματα.

Οι λύσεις θα είναι όλα τα σημεία του μοναδιαίου κύκλου που ανήκουν στο τόξο l Ας βρούμε τα σημεία t1 και t2.
t1 = arccos(1/2) = pi/3.
t2 = 2*pi - arccos(1/2) = 2*pi-pi/3 = 5*pi/6.
Πήραμε την ανισότητα για t: pi/3 Δεδομένου ότι το συνημίτονο είναι περιοδική συνάρτηση, οι λύσεις θα επαναλαμβάνονται κάθε 2*pi. Προσθέτουμε αυτή τη συνθήκη στην προκύπτουσα ανισότητα για το t και γράφουμε την απάντηση. Απάντηση: pi/3+2*pi*n Παράδειγμα 3.Επίλυση ανισότητας tg(t)< = 1. Η εφαπτομένη περίοδος είναι ίση με το pi. Ας βρούμε λύσεις που ανήκουν στο διάστημα (-pi/2;pi/2) δεξιό ημικύκλιο. Στη συνέχεια, χρησιμοποιώντας την περιοδικότητα της εφαπτομένης, γράφουμε όλες τις λύσεις αυτής της ανισότητας. Ας σχεδιάσουμε έναν μοναδιαίο κύκλο και ας σημειώσουμε μια ευθεία εφαπτομένων πάνω του. Εάν το t είναι λύση στην ανίσωση, τότε η τεταγμένη του σημείου T = tg(t) πρέπει να είναι μικρότερη ή ίση με 1. Το σύνολο τέτοιων σημείων θα αποτελέσει την ακτίνα ΑΤ. Το σύνολο των σημείων Pt που θα αντιστοιχεί στα σημεία αυτής της ακτίνας είναι το τόξο l. Επιπλέον, το σημείο P(-pi/2) δεν ανήκει σε αυτό το τόξο. Οι ανισότητες είναι σχέσεις της μορφής a › b, όπου a και b είναι εκφράσεις που περιέχουν τουλάχιστον μία μεταβλητή. Οι ανισότητες μπορεί να είναι αυστηρές - ‹, › και μη αυστηρές - ≥, ≤. Οι τριγωνομετρικές ανισότητες είναι εκφράσεις της μορφής: F(x) › a, F(x) ‹ a, F(x) ≤ a, F(x) ≥ a, στις οποίες η F(x) αντιπροσωπεύεται από μία ή περισσότερες τριγωνομετρικές συναρτήσεις . Ένα παράδειγμα της απλούστερης τριγωνομετρικής ανισότητας είναι: sin x ‹ 1/2. Είναι σύνηθες να επιλύονται τέτοια προβλήματα γραφικά, έχουν αναπτυχθεί δύο μέθοδοι. Για να βρείτε ένα διάστημα που να ικανοποιεί τις συνθήκες της ανισότητας sin x ‹ 1/2, πρέπει να εκτελέσετε τα ακόλουθα βήματα: Όταν υπάρχουν αυστηρά σημάδια σε μια έκφραση, τα σημεία τομής δεν είναι λύσεις. Επειδή η μικρότερη θετική περίοδος ενός ημιτονοειδούς είναι 2π, γράφουμε την απάντηση ως εξής: Εάν τα σημάδια της έκφρασης δεν είναι αυστηρά, τότε το διάστημα επίλυσης πρέπει να περικλείεται σε αγκύλες - . Η απάντηση στο πρόβλημα μπορεί επίσης να γραφτεί ως η ακόλουθη ανισότητα: Παρόμοια προβλήματα μπορούν εύκολα να λυθούν χρησιμοποιώντας έναν τριγωνομετρικό κύκλο. Ο αλγόριθμος για την εύρεση απαντήσεων είναι πολύ απλός: Ας αναλύσουμε τα στάδια της λύσης χρησιμοποιώντας το παράδειγμα της ανισότητας sin x › 1/2. Τα σημεία α και β σημειώνονται στον κύκλο - τιμές Τα σημεία του τόξου που βρίσκονται πάνω από το α και το β είναι το διάστημα για την επίλυση της δεδομένης ανισότητας. Εάν πρέπει να λύσετε ένα παράδειγμα για το cos, τότε το τόξο απάντησης θα βρίσκεται συμμετρικά προς τον άξονα OX, όχι OY. Μπορείτε να εξετάσετε τη διαφορά μεταξύ των διαστημάτων λύσης για το sin και το cos στα παρακάτω διαγράμματα του κειμένου. Οι γραφικές λύσεις για τις εφαπτομενικές και συνεφαπτομενικές ανισότητες θα διαφέρουν τόσο από ημιτονοειδές όσο και από συνημίτονο. Αυτό οφείλεται στις ιδιότητες των συναρτήσεων. Η τοξοεφαπτομένη είναι εφαπτομένη σε έναν τριγωνομετρικό κύκλο και η ελάχιστη θετική περίοδος και για τις δύο συναρτήσεις είναι π. Για να χρησιμοποιήσετε γρήγορα και σωστά τη δεύτερη μέθοδο, πρέπει να θυμάστε σε ποιον άξονα απεικονίζονται οι τιμές sin, cos, tg και ctg. Η εφαπτομένη είναι παράλληλη με τον άξονα OY. Εάν σχεδιάσουμε την τιμή του αρκτανίου a στον μοναδιαίο κύκλο, τότε το δεύτερο απαιτούμενο σημείο θα βρίσκεται στο διαγώνιο τέταρτο. Γωνίες Είναι σημεία διακοπής για τη συνάρτηση, αφού το γράφημα τείνει προς αυτά, αλλά δεν τα φτάνει ποτέ. Στην περίπτωση της συνεφαπτομένης, η εφαπτομένη είναι παράλληλη προς τον άξονα ΟΧ και η συνάρτηση διακόπτεται στα σημεία π και 2π. Εάν το όρισμα της συνάρτησης ανισότητας αντιπροσωπεύεται όχι μόνο από μια μεταβλητή, αλλά από μια ολόκληρη παράσταση που περιέχει έναν άγνωστο, τότε μιλάμε για μια σύνθετη ανισότητα. Η διαδικασία και η διαδικασία επίλυσής του διαφέρουν κάπως από τις μεθόδους που περιγράφονται παραπάνω. Ας υποθέσουμε ότι πρέπει να βρούμε μια λύση στην ακόλουθη ανισότητα: Η γραφική λύση περιλαμβάνει την κατασκευή ενός συνηθισμένου ημιτονοειδούς y = sin x χρησιμοποιώντας αυθαίρετα επιλεγμένες τιμές του x. Ας υπολογίσουμε έναν πίνακα με συντεταγμένες για τα σημεία ελέγχου του γραφήματος: Το αποτέλεσμα πρέπει να είναι μια όμορφη καμπύλη. Για να διευκολύνουμε την εύρεση λύσης, ας αντικαταστήσουμε το όρισμα σύνθετης συνάρτησης Στους περισσότερους μαθητές δεν αρέσουν οι τριγωνομετρικές ανισότητες. Μάταια όμως. Όπως έλεγε ένας χαρακτήρας, «Απλά δεν ξέρεις πώς να τα μαγειρέψεις» Λοιπόν, πώς να «μαγειρέψουμε» και με τι να υποβάλουμε ανισότητα με ημιτονοειδή θα καταλάβουμε σε αυτό το άρθρο. Θα το λύσουμε με τον απλούστερο τρόπο - χρησιμοποιώντας τον κύκλο μονάδας. Άρα, πρώτα από όλα χρειαζόμαστε τον ακόλουθο αλγόριθμο. Σημαντικό: δδεδομένου αλγόριθμου δεν λειτουργείγια ανισώσεις της μορφής $\sin(x) > 1; \ \sin(x) \geq 1, \ \sin(x)< -1, \ \sin{x} \leq -1$. В строгом случае эти неравенства не имеют решений, а в нестрогом – решение сводится к решению уравнения $\sin{x} = 1$ или $\sin{x} = -1$. Είναι επίσης σημαντικό να σημειωθούν οι ακόλουθες περιπτώσεις, οι οποίες είναι πολύ πιο βολικό να επιλυθούν λογικά χωρίς τη χρήση του παραπάνω αλγόριθμου. Ειδική περίπτωση 1.Επίλυση ανισότητας: $\sin(x)\leq 1.$ Λόγω του γεγονότος ότι το εύρος τιμών της τριγωνομετρικής συνάρτησης $y=\sin(x)$ δεν είναι μεγαλύτερο από το modulo $1$, τότε η αριστερή πλευρά της ανισότητας σε οποιαδήποτεΤο $x$ από το πεδίο ορισμού (και το πεδίο ορισμού του ημιτόνου είναι όλοι πραγματικοί αριθμοί) δεν υπερβαίνει το $1$. Αυτό σημαίνει ότι γράφουμε την απάντηση: $x \σε R$. Συνέπεια: $\sin(x)\geq -1.$ Ειδική περίπτωση 2.Επίλυση ανισότητας: $\sin(x)< 1.$ Εφαρμόζοντας συλλογισμό παρόμοιο με την ειδική περίπτωση 1, βρίσκουμε ότι η αριστερή πλευρά της ανισότητας είναι μικρότερη από $1$ για όλα τα $x \σε R$, εκτός από τα σημεία που είναι λύσεις στην εξίσωση $\sin(x) = 1$. Λύνοντας αυτή την εξίσωση θα έχουμε: $x = (-1)^(n)\arcsin(1)+ \pi n = (-1)^(n)\frac(\pi)(2) + \pi n.$ Και, επομένως, στην απάντηση γράφουμε: $x \in R \backslash \left\((-1)^(n)\frac(\pi)(2) + \pi n\right\)$. Συνέπεια:η ανισότητα λύνεται ομοίως $\sin(x) > -1.$ Παράδειγμα 1:Επίλυση ανισότητας: $\sin(x) \geq \frac(1)(2).$ Έτσι, η λύση θα έχει τη μορφή: $x \in \left[\frac(\pi)(6) + 2\pi n; \frac(5\pi)(6) + 2 \pi n\right], \n \σε Z.$ Παράδειγμα 2:Επίλυση ανισότητας: $\sin(x)< -\frac{1}{2}$ Ας σημειώσουμε τη συντεταγμένη $-\frac(1)(2)$ στον ημιτονοειδή άξονα και ας σχεδιάσουμε μια ευθεία γραμμή παράλληλη προς τον άξονα συνημιτόνου και που διέρχεται από αυτό το σημείο. Ας σημειώσουμε τα σημεία τομής. Δεν θα σκιαστούν, αφού η ανισότητα είναι αυστηρή. Το σύμβολο της ανισότητας $<$, а, значит, закрашиваем область ниже прямой, т.е. меньший полукруг. Неравенство превращаем в равенство и решаем его: $\sin(x)=-\frac(1)(2)$ $x=(-1)^(n)\arcsin(\left(-\frac(1)(2)\right))+ \pi n =(-1)^(n+1)\frac(\pi )(6) + \pi n$. Περαιτέρω υποθέτοντας $n=0$, βρίσκουμε το πρώτο σημείο τομής: $x_(1)=-\frac(\pi)(6)$. Η περιοχή μας πηγαίνει προς την αρνητική κατεύθυνση από το πρώτο σημείο, που σημαίνει ότι ορίζουμε $n$ ίσο με $-1$: $x_(2)=(-1)^(-1+1)\frac(\pi)( 6) + \pi \cdot (-1) = -\pi + \frac(\pi)(6) = -\frac(5\pi)(6)$. $x \in \left(-\frac(5\pi)(6) + 2\pi n; -\frac(\pi)(6) + 2 \pi n\right), \n \in Z.$ Παράδειγμα 3:Επίλυση ανισότητας: $1 – 2\sin(\left(\frac(x)(4)+\frac(\pi)(6)\right)) \leq 0.$ Αυτό το παράδειγμα δεν μπορεί να λυθεί αμέσως χρησιμοποιώντας έναν αλγόριθμο. Πρώτα πρέπει να το μεταμορφώσεις. Κάνουμε ακριβώς αυτό που θα κάναμε με μια εξίσωση, αλλά μην ξεχνάτε το ζώδιο. Η διαίρεση ή ο πολλαπλασιασμός με έναν αρνητικό αριθμό τον αντιστρέφει! Ας μετακινήσουμε, λοιπόν, όλα όσα δεν περιέχουν τριγωνομετρική συνάρτηση στη δεξιά πλευρά. Παίρνουμε: $ - 2\sin(\left(\frac(x)(4)+\frac(\pi)(6)\right)) \leq -1.$ Ας διαιρέσουμε την αριστερή και τη δεξιά πλευρά με $-2$ (μην ξεχνάτε το σημάδι!). θα έχουμε: $\sin(\left(\frac(x)(4)+\frac(\pi)(6)\right)) \geq \frac(1)(2).$ Και πάλι έχουμε μια ανισότητα που δεν μπορούμε να λύσουμε χρησιμοποιώντας έναν αλγόριθμο. Αλλά εδώ αρκεί να αλλάξετε τη μεταβλητή: $t=\frac(x)(4)+\frac(\pi)(6).$ Λαμβάνουμε μια τριγωνομετρική ανισότητα που μπορεί να λυθεί χρησιμοποιώντας τον αλγόριθμο: $\sin(t) \geq \frac(1)(2).$ Αυτή η ανισότητα λύθηκε στο Παράδειγμα 1, οπότε ας δανειστούμε την απάντηση από εκεί: $t \in \left[\frac(\pi)(6) + 2\pi n; \frac(5\pi)(6) + 2 \pi n\right].$ Ωστόσο, η απόφαση δεν έχει τελειώσει ακόμη. Πρέπει να επιστρέψουμε στην αρχική μεταβλητή. $(\frac(x)(4)+\frac(\pi)(6)) \in \left[\frac(\pi)(6) + 2\pi n; \frac(5\pi)(6) + 2 \pi n\right].$ Ας φανταστούμε το διάστημα ως σύστημα: $\left\(\begin(array)(c) \frac(x)(4)+\frac(\pi)(6) \geq \frac(\pi)(6) + 2\pi n, \\ \frac(x)(4)+\frac(\pi)(6) \leq \frac(5\pi)(6) + 2 \pi n \right.$ Στην αριστερή πλευρά του συστήματος υπάρχει μια έκφραση ($\frac(x)(4)+\frac(\pi)(6)$), η οποία ανήκει στο διάστημα. Το αριστερό όριο του διαστήματος είναι υπεύθυνο για την πρώτη ανισότητα και το δεξί όριο είναι υπεύθυνο για τη δεύτερη. Επιπλέον, οι αγκύλες διαδραματίζουν σημαντικό ρόλο: εάν η αγκύλη είναι τετράγωνη, τότε η ανισότητα θα χαλαρώσει και εάν είναι στρογγυλή, τότε θα είναι αυστηρή. Το καθήκον μας είναι να πάρουμε $x$ στα αριστερά και στις δύο ανισότητες. Ας μετακινήσουμε το $\frac(\pi)(6)$ από την αριστερή πλευρά στη δεξιά πλευρά, παίρνουμε: $\left\(\begin(array)(c) \frac(x)(4) \geq \frac(\pi)(6) + 2\pi n -\frac(\pi)(6), \\ \frac(x)(4) \leq \frac(5\pi)(6) + 2 \pi n – \frac(\pi)(6) \end(array) \right.$. Απλοποιώντας, θα έχουμε: $\left\(\begin(array)(c) \frac(x)(4) \geq 2\pi n, \\ \frac(x)(4) \leq \frac(2\pi)(3) + 2 \pi n \end(πίνακας) \right.$ Πολλαπλασιάζοντας την αριστερή και τη δεξιά πλευρά με $4$, παίρνουμε: $\left\(\begin(array)(c) x \geq 8\pi n, \\ x \leq \frac(8\pi)(3) + 8 \pi n. \end(array) \right. $ Συναρμολογώντας το σύστημα στο διάστημα, παίρνουμε την απάντηση: $x \in \left[ 8\pi n; \frac(8\pi)(3) + 8 \pi n\right], \n \σε Z.$ ΜΕΘΟΔΟΙ ΕΠΙΛΥΣΗΣ ΤΡΙΓΩΝΟΜΕΤΡΙΚΩΝ ΑΝΙΣΟΤΗΤΩΝ
Συνάφεια.
Ιστορικά, οι τριγωνομετρικές εξισώσεις και οι ανισότητες έχουν δοθεί ιδιαίτερη θέση στο σχολικό πρόγραμμα σπουδών. Μπορούμε να πούμε ότι η τριγωνομετρία είναι ένα από τα σημαντικότερα τμήματα του σχολικού μαθήματος και ολόκληρης της μαθηματικής επιστήμης γενικότερα. Οι τριγωνομετρικές εξισώσεις και οι ανισότητες καταλαμβάνουν μία από τις κεντρικές θέσεις στο μάθημα των μαθηματικών της δευτεροβάθμιας εκπαίδευσης, τόσο στο περιεχόμενο εκπαιδευτικό υλικό, και σύμφωνα με τις μεθόδους εκπαιδευτικής και γνωστικής δραστηριότητας, που μπορούν και πρέπει να διαμορφωθούν κατά τη διάρκεια της μελέτης τους και να εφαρμοστούν στην επίλυση μεγάλου αριθμού προβλημάτων θεωρητικής και εφαρμοσμένης φύσης. Η επίλυση τριγωνομετρικών εξισώσεων και ανισώσεων δημιουργεί τις προϋποθέσεις για τη συστηματοποίηση των γνώσεων των μαθητών που σχετίζονται με όλο το εκπαιδευτικό υλικό στην τριγωνομετρία (για παράδειγμα, ιδιότητες τριγωνομετρικών συναρτήσεων, μέθοδοι μετασχηματισμού τριγωνομετρικών εκφράσεων κ.λπ.) και καθιστά δυνατή τη δημιουργία αποτελεσματικών συνδέσεων με το μελετώμενο υλικό στην άλγεβρα (εξισώσεις, ισοδυναμία εξισώσεων, ανισώσεις, πανομοιότυποι μετασχηματισμοί αλγεβρικών παραστάσεων κ.λπ.). Με άλλα λόγια, η εξέταση τεχνικών για την επίλυση τριγωνομετρικών εξισώσεων και ανισοτήτων περιλαμβάνει ένα είδος μεταφοράς αυτών των δεξιοτήτων σε νέο περιεχόμενο. Η σημασία της θεωρίας και οι πολυάριθμες εφαρμογές της είναι απόδειξη της συνάφειας του επιλεγμένου θέματος. Αυτό με τη σειρά του σας επιτρέπει να προσδιορίσετε τους στόχους, τους στόχους και το αντικείμενο έρευνας της εργασίας του μαθήματος. Σκοπός της μελέτης:
γενικεύστε τους διαθέσιμους τύπους τριγωνομετρικών ανισώσεων, βασικές και ειδικές μεθόδους επίλυσής τους, επιλέξτε ένα σύνολο προβλημάτων για την επίλυση τριγωνομετρικών ανισοτήτων από μαθητές. Στόχοι της έρευνας:
1. Με βάση την ανάλυση της διαθέσιμης βιβλιογραφίας για το ερευνητικό θέμα, συστηματοποιήστε το υλικό. 2. Παρέχετε ένα σύνολο εργασιών που είναι απαραίτητες για την εδραίωση του θέματος «Τριγωνομετρικές ανισότητες». Αντικείμενο μελέτης
είναι τριγωνομετρικές ανισότητες στο μάθημα των σχολικών μαθηματικών. Αντικείμενο έρευνας:
είδη τριγωνομετρικών ανισώσεων και μέθοδοι επίλυσής τους. Θεωρητική σημασία
είναι η συστηματοποίηση του υλικού. Πρακτική σημασία:
εφαρμογή της θεωρητικής γνώσης στην επίλυση προβλημάτων. ανάλυση των κύριων κοινών μεθόδων για την επίλυση τριγωνομετρικών ανισώσεων. Μέθοδοι έρευνας
: ανάλυση επιστημονικής βιβλιογραφίας, σύνθεση και γενίκευση της αποκτηθείσας γνώσης, ανάλυση επίλυσης προβλημάτων, αναζήτηση βέλτιστων μεθόδων επίλυσης ανισοτήτων. §1.
Είδη τριγωνομετρικών ανισώσεων και βασικές μέθοδοι επίλυσής τους
1.1. Οι απλούστερες τριγωνομετρικές ανισώσεις
Δύο τριγωνομετρικές εκφράσεις που συνδέονται με το πρόσημο ή > ονομάζονται τριγωνομετρικές ανισότητες. Η επίλυση μιας τριγωνομετρικής ανισότητας σημαίνει την εύρεση του συνόλου των τιμών των αγνώστων που περιλαμβάνονται στην ανισότητα για την οποία ικανοποιείται η ανισότητα. Το κύριο μέρος των τριγωνομετρικών ανισώσεων λύνεται με την αναγωγή τους στην απλούστερη λύση: Αυτή μπορεί να είναι μια μέθοδος παραγοντοποίησης, αλλαγής μεταβλητής ( Οι απλούστερες ανισώσεις μπορούν να λυθούν με δύο τρόπους: χρησιμοποιώντας τον κύκλο μονάδας ή γραφικά. Αφήνωf(x
– μία από τις βασικές τριγωνομετρικές συναρτήσεις. Για να λύσουμε την ανισότητα Ας δώσουμε ένα παράδειγμα αλγορίθμου για την επίλυση ανισώσεων Αλγόριθμος για την επίλυση της ανισότητας 1. Να διατυπώσετε τον ορισμό του ημίτονου ενός αριθμούx
στον κύκλο της μονάδας. 3. Στον άξονα τεταγμένων σημειώνουμε το σημείο με τη συντεταγμένηένα
.
4. Σχεδιάστε μια ευθεία παράλληλη προς τον άξονα OX μέσω αυτού του σημείου και σημειώστε τα σημεία τομής του με τον κύκλο. 5. Επιλέξτε ένα τόξο ενός κύκλου, του οποίου όλα τα σημεία έχουν τεταγμένη μικρότερη απόένα
.
6. Υποδείξτε την κατεύθυνση του γύρου (αριστερόστροφα) και σημειώστε την απάντηση προσθέτοντας την περίοδο της συνάρτησης στα άκρα του διαστήματος2πn
,
Αλγόριθμος για την επίλυση της ανισότητας 1. Να διατυπώσετε τον ορισμό της εφαπτομένης ενός αριθμούx
στον κύκλο της μονάδας. 2. Σχεδιάστε έναν κύκλο μονάδας. 3. Σχεδιάστε μια ευθεία εφαπτομένων και σημειώστε ένα σημείο με μια τεταγμένη πάνω τηςένα
.
4. Συνδέστε αυτό το σημείο με την αρχή και σημειώστε το σημείο τομής του τμήματος που προκύπτει με τον μοναδιαίο κύκλο. 5. Επιλέξτε τόξο κύκλου, όλα τα σημεία του οποίου έχουν τεταγμένη στην εφαπτομένη ευθεία μικρότερη απόένα
.
6. Υποδείξτε την κατεύθυνση της διέλευσης και γράψτε την απάντηση λαμβάνοντας υπόψη το πεδίο ορισμού της συνάρτησης, προσθέτοντας μια τελείαπn
,
Η γραφική ερμηνεία των λύσεων των απλούστερων εξισώσεων και οι τύποι για την επίλυση ανισώσεων σε γενική μορφή αναφέρονται στο παράρτημα (Παραρτήματα 1 και 2). Παράδειγμα 1.
Λύστε την ανισότητα Σχεδιάστε μια ευθεία γραμμή στον κύκλο της μονάδας Όλες οι έννοιεςy
στο διάστημα το NM είναι μεγαλύτερο
, όλα τα σημεία του τόξου AMB ικανοποιούν αυτήν την ανισότητα. Σε όλες τις γωνίες περιστροφής, μεγάλες Εικ.1 Έτσι, η λύση της ανισότητας θα είναι όλες οι τιμές στο διάστημα εκείνοι. Απάντηση: 1.2. Γραφική μέθοδος
Στην πράξη, η γραφική μέθοδος για την επίλυση τριγωνομετρικών ανισώσεων αποδεικνύεται συχνά χρήσιμη. Ας εξετάσουμε την ουσία της μεθόδου χρησιμοποιώντας το παράδειγμα της ανισότητας 1. Εάν το όρισμα είναι σύνθετο (διαφορετικό απόΧ
), στη συνέχεια αντικαταστήστε το μεt
.
2. Χτίζουμε σε ένα επίπεδο συντεταγμένωνπαιχνίδι
γραφήματα συναρτήσεων 3. Βρίσκουμε τέτοιαδύο γειτονικά σημεία τομής γραφημάτων, μεταξύ των οποίωνημιτονοειδές κύμαπου βρίσκεταιυψηλότερα
απευθείας 4. Γράψτε μια διπλή ανισότητα για το όρισμαt
λαμβάνοντας υπόψη την περίοδο συνημιτόνου (t
θα είναι μεταξύ των ευρεθέντων τετμητών). 5. Κάντε μια αντίστροφη αντικατάσταση (επιστροφή στο αρχικό όρισμα) και εκφράστε την τιμήΧ
από τη διπλή ανισότητα, γράφουμε την απάντηση με τη μορφή αριθμητικού διαστήματος. Παράδειγμα 2.
Επίλυση ανισότητας: . Κατά την επίλυση ανισώσεων χρησιμοποιώντας τη γραφική μέθοδο, είναι απαραίτητο να κατασκευαστούν γραφήματα συναρτήσεων όσο το δυνατόν ακριβέστερα. Ας μετατρέψουμε την ανισότητα στη μορφή: Ας κατασκευάσουμε γραφήματα συναρτήσεων σε ένα σύστημα συντεταγμένων Εικ.2 Οι γραφικές παραστάσεις των συναρτήσεων τέμνονται στο σημείοΕΝΑ
με συντεταγμένες Απάντηση: 1.3. Αλγεβρική μέθοδος
Αρκετά συχνά, η αρχική τριγωνομετρική ανισότητα μπορεί να μειωθεί σε αλγεβρική (ορθολογική ή παράλογη) ανισότητα μέσω μιας καλά επιλεγμένης αντικατάστασης. Αυτή η μέθοδος περιλαμβάνει τον μετασχηματισμό μιας ανισότητας, την εισαγωγή μιας αντικατάστασης ή την αντικατάσταση μιας μεταβλητής. Ας δούμε συγκεκριμένα παραδείγματα εφαρμογής αυτής της μεθόδου. Παράδειγμα 3.
Αναγωγή στην απλούστερη μορφή Εικ.3 Απάντηση: Παράδειγμα 4.
Επίλυση ανισότητας: ODZ: Χρησιμοποιώντας τύπους: Ας γράψουμε την ανισότητα με τη μορφή: Ή, πιστεύοντας Επιλύοντας την τελευταία ανισότητα χρησιμοποιώντας τη μέθοδο του διαστήματος, παίρνουμε: Εικ.4 Εικ.5 Απάντηση: 1.4. Μέθοδος διαστήματος
Γενικό σχήμα για την επίλυση τριγωνομετρικών ανισώσεων με τη μέθοδο του διαστήματος: Παράγοντας με χρήση τριγωνομετρικών τύπων. Βρείτε τα σημεία ασυνέχειας και τα μηδενικά της συνάρτησης και τοποθετήστε τα στον κύκλο. Πάρτε οποιοδήποτε σημείοΝΑ
(αλλά δεν βρέθηκε νωρίτερα) και μάθετε το σήμα του προϊόντος. Εάν το προϊόν είναι θετικό, τότε τοποθετήστε ένα σημείο έξω από τον κύκλο μονάδας στην ακτίνα που αντιστοιχεί στη γωνία. Διαφορετικά, τοποθετήστε το σημείο μέσα στον κύκλο. Εάν ένα σημείο εμφανίζεται άρτιος αριθμός φορών, το ονομάζουμε σημείο άρτιου πολλαπλασιασμού, αν είναι περιττό, το ονομάζουμε σημείο περιττής πολλαπλότητας. Σχεδιάστε τόξα ως εξής: ξεκινήστε από ένα σημείοΝΑ
, αν το επόμενο σημείο είναι περιττής πολλαπλότητας, τότε το τόξο τέμνει τον κύκλο σε αυτό το σημείο, αλλά αν το σημείο είναι άρτιου πολλαπλότητας, τότε δεν τέμνεται. Τα τόξα πίσω από τον κύκλο είναι θετικά διαστήματα. μέσα στον κύκλο υπάρχουν αρνητικά κενά. Παράδειγμα 5.
Λύστε την ανισότητα Σημεία της πρώτης σειράς: Σημεία της δεύτερης σειράς: Κάθε σημείο εμφανίζεται μονές φορές, δηλαδή όλα τα σημεία είναι περιττής πολλαπλότητας. Ας μάθουμε το σήμα του προϊόντος στο Ρύζι. 6 Απάντηση: Παράδειγμα 6
. Λύστε την ανισότητα.
Διάλυμα:
Ας βρούμε τα μηδενικά της έκφρασης .
Λαμβάνωαεm :
Στις τιμές της σειράς κύκλου μονάδαςΧ
1
παριστάνεται με τελείες Αφήστε τώρα τον αριθμό Λοιπόν τελείαΕΝΑ
πρέπει να επιλεγεί στην ακτίνα που σχηματίζει τη γωνία Τώρα από το σημείοΕΝΑ
σχεδιάστε μια κυματιστή συνεχή γραμμή διαδοχικά σε όλα τα σημειωμένα σημεία. Και σε σημεία Εικ.7 Τελική απάντηση: Σημείωμα.
Εάν μια κυματιστή γραμμή, αφού διασχίσει όλα τα σημεία που σημειώνονται στον κύκλο μονάδας, δεν μπορεί να επιστρέψει στο σημείοΕΝΑ
,
χωρίς να διασχίσετε τον κύκλο σε "παράνομο" μέρος, αυτό σημαίνει ότι έγινε σφάλμα στη λύση, δηλαδή, χάθηκε ένας περιττός αριθμός ριζών. Απάντηση:
.
§2. Ένα σύνολο προβλημάτων για την επίλυση τριγωνομετρικών ανισώσεων
Στη διαδικασία ανάπτυξης της ικανότητας των μαθητών να λύνουν τριγωνομετρικές ανισότητες, μπορούν επίσης να διακριθούν 3 στάδια. 1. προπαρασκευαστική, 2. ανάπτυξη της ικανότητας επίλυσης απλών τριγωνομετρικών ανισώσεων. 3. εισαγωγή τριγωνομετρικών ανισώσεων άλλων τύπων. Ο σκοπός του προπαρασκευαστικού σταδίου είναι ότι είναι απαραίτητο να αναπτυχθεί στους μαθητές η ικανότητα χρήσης τριγωνομετρικού κύκλου ή γραφήματος για την επίλυση ανισοτήτων, και συγκεκριμένα: Ικανότητα επίλυσης απλών ανισώσεων της φόρμας Δυνατότητα κατασκευής διπλών ανισώσεων για τόξα του κύκλου αριθμών ή για τόξα γραφημάτων συναρτήσεων. Δυνατότητα εκτέλεσης διαφόρων μετασχηματισμών τριγωνομετρικών παραστάσεων. Συνιστάται η εφαρμογή αυτού του σταδίου στη διαδικασία συστηματοποίησης της γνώσης των μαθητών σχετικά με τις ιδιότητες των τριγωνομετρικών συναρτήσεων. Τα κύρια μέσα μπορεί να είναι εργασίες που προσφέρονται στους μαθητές και εκτελούνται είτε υπό την καθοδήγηση ενός δασκάλου είτε ανεξάρτητα, καθώς και δεξιότητες που αναπτύσσονται στην επίλυση τριγωνομετρικών εξισώσεων. Ακολουθούν παραδείγματα τέτοιων εργασιών: 1
. Σημειώστε ένα σημείο στον κύκλο της μονάδας .
2.
Σε ποιο τέταρτο του επιπέδου συντεταγμένων βρίσκεται το σημείο; 3.
Σημειώστε τα σημεία στον τριγωνομετρικό κύκλο 4.
Μετατρέψτε την έκφραση σε τριγωνομετρικές συναρτήσειςεγώκατάλυμα. ΕΝΑ) 5.
Δίνεται τόξο MR.Μ
– μέσηεγώ-ο τρίμηνο,R
– μέσηIIτο τρίμηνο. Περιορίστε την τιμή μιας μεταβλητήςt
για: (κάντε διπλή ανισότητα) α) τόξο MR; β) τόξα RM. 6.
Γράψτε τη διπλή ανισότητα για τα επιλεγμένα τμήματα του γραφήματος: Ρύζι. 1 7.
Λύστε ανισότητες 8.
Μετατροπή έκφρασης
.
Στο δεύτερο στάδιο της εκμάθησης επίλυσης τριγωνομετρικών ανισοτήτων, μπορούμε να προσφέρουμε τις ακόλουθες συστάσεις σχετικά με τη μεθοδολογία οργάνωσης των δραστηριοτήτων των μαθητών. Σε αυτή την περίπτωση, είναι απαραίτητο να εστιάσουμε στις υπάρχουσες δεξιότητες των μαθητών στην εργασία με έναν τριγωνομετρικό κύκλο ή γράφημα, που σχηματίζεται κατά την επίλυση των απλούστερων τριγωνομετρικών εξισώσεων. Πρώτον, μπορεί κανείς να παρακινήσει τη σκοπιμότητα απόκτησης μιας γενικής μεθόδου για την επίλυση των απλούστερων τριγωνομετρικών ανισώσεων στρέφοντας, για παράδειγμα, σε μια ανισότητα της μορφής Δεύτερον, ο δάσκαλος πρέπει να επιστήσει την προσοχή των μαθητών σε διαφορετικούς τρόπους ολοκλήρωσης της εργασίας, να δώσει ένα κατάλληλο παράδειγμα επίλυσης της ανισότητας τόσο γραφικά όσο και χρησιμοποιώντας έναν τριγωνομετρικό κύκλο. Ας εξετάσουμε τις παρακάτω λύσεις για την ανισότητα 1. Επίλυση της ανίσωσης χρησιμοποιώντας τον μοναδιαίο κύκλο. Στο πρώτο μάθημα επίλυσης τριγωνομετρικών ανισώσεων, θα προσφέρουμε στους μαθητές έναν λεπτομερή αλγόριθμο επίλυσης, ο οποίος σε μια βήμα προς βήμα παρουσίαση αντικατοπτρίζει όλες τις βασικές δεξιότητες που είναι απαραίτητες για την επίλυση της ανισότητας. Βήμα 1.Ας σχεδιάσουμε έναν κύκλο μονάδας και ας σημειώσουμε ένα σημείο στον άξονα τεταγμένων Βήμα 2.Αυτή η ευθεία χώριζε τον κύκλο σε δύο τόξα. Ας επιλέξουμε αυτόν που απεικονίζει αριθμούς που έχουν ημίτονο μεγαλύτερο από Ρύζι. 2 Βήμα 3.Επιλέξτε ένα από τα άκρα του σημειωμένου τόξου. Ας γράψουμε έναν από τους αριθμούς που αντιπροσωπεύεται από αυτό το σημείο του κύκλου μονάδας Βήμα 4.Για να επιλέξουμε τον αριθμό που αντιστοιχεί στο δεύτερο άκρο του επιλεγμένου τόξου, «περπατάμε» κατά μήκος αυτού του τόξου από το ονομασμένο άκρο στο άλλο. Ταυτόχρονα, θυμηθείτε ότι όταν κινούμαστε αριστερόστροφα, οι αριθμοί που θα προσπεράσουμε αυξάνονται (όταν κινούμαστε προς την αντίθετη κατεύθυνση, οι αριθμοί θα μειώνονταν). Ας γράψουμε τον αριθμό που απεικονίζεται στον μοναδιαίο κύκλο στο δεύτερο άκρο του σημειωμένου τόξου Έτσι, βλέπουμε αυτή την ανισότητα Θα πρέπει να ζητηθεί από τους μαθητές να εξετάσουν προσεκτικά το σχέδιο και να καταλάβουν γιατί όλες οι λύσεις στην ανισότητα Ρύζι. 3 Είναι απαραίτητο να επιστήσουμε την προσοχή των μαθητών στο γεγονός ότι κατά την επίλυση ανισώσεων για τη συνάρτηση συνημιτόνου, σχεδιάζουμε μια ευθεία παράλληλη προς τον άξονα των τεταγμένων. Γραφική μέθοδος επίλυσης ανισώσεων. Κατασκευάζουμε γραφήματα Ρύζι. 4 Στη συνέχεια γράφουμε την εξίσωση (Χορήγησηn
τιμές 0, 1, 2, βρίσκουμε τις τρεις ρίζες της μεταγλωττισμένης εξίσωσης). Αξίες Ρύζι. 5 Ας συνοψίσουμε. Για να λύσουμε την ανισότητα Τρίτον, το γεγονός σχετικά με το σύνολο των ριζών της αντίστοιχης τριγωνομετρικής ανισότητας επιβεβαιώνεται πολύ καθαρά όταν το λύνουμε γραφικά. Ρύζι. 6 Είναι απαραίτητο να δείξουμε στους μαθητές ότι η στροφή, που είναι η λύση της ανίσωσης, επαναλαμβάνεται στο ίδιο διάστημα, ίσο με την περίοδο της τριγωνομετρικής συνάρτησης. Μπορείτε επίσης να εξετάσετε μια παρόμοια απεικόνιση για το γράφημα της συνάρτησης ημιτόνου. Τέταρτον, είναι σκόπιμο να πραγματοποιηθεί εργασία για την ενημέρωση των τεχνικών των μαθητών για τη μετατροπή του αθροίσματος (διαφοράς) των τριγωνομετρικών συναρτήσεων σε γινόμενο και να επιστήσουμε την προσοχή των μαθητών στο ρόλο αυτών των τεχνικών στην επίλυση τριγωνομετρικών ανισοτήτων. Μια τέτοια εργασία μπορεί να οργανωθεί μέσω της ανεξάρτητης ολοκλήρωσης των εργασιών που προτείνει ο δάσκαλος από τους μαθητές, μεταξύ των οποίων επισημαίνουμε τα ακόλουθα: Πέμπτον, πρέπει να ζητηθεί από τους μαθητές να επεξηγήσουν τη λύση σε κάθε απλή τριγωνομετρική ανισότητα χρησιμοποιώντας ένα γράφημα ή έναν τριγωνομετρικό κύκλο. Πρέπει οπωσδήποτε να δώσετε προσοχή στη σκοπιμότητά του, ειδικά στη χρήση κύκλου, καθώς κατά την επίλυση τριγωνομετρικών ανισώσεων, η αντίστοιχη απεικόνιση χρησιμεύει ως πολύ βολικό μέσο καταγραφής του συνόλου λύσεων σε μια δεδομένη ανισότητα Συνιστάται να εισαγάγετε τους μαθητές σε μεθόδους επίλυσης τριγωνομετρικών ανισώσεων που δεν είναι οι απλούστερες σύμφωνα με το ακόλουθο σχήμα: στροφή σε μια συγκεκριμένη τριγωνομετρική ανισότητα στροφή στην αντίστοιχη τριγωνομετρική εξίσωση κοινή αναζήτηση (δάσκαλος - μαθητές) για μια λύση ανεξάρτητη μεταφορά του βρέθηκε μέθοδος σε άλλες ανισότητες του ίδιου τύπου. Προκειμένου να συστηματοποιηθούν οι γνώσεις των μαθητών σχετικά με την τριγωνομετρία, συνιστούμε την ειδική επιλογή τέτοιων ανισοτήτων, η επίλυση των οποίων απαιτεί διάφορους μετασχηματισμούς που μπορούν να εφαρμοστούν κατά τη διαδικασία επίλυσής της και να επικεντρωθεί η προσοχή των μαθητών στα χαρακτηριστικά τους. Ως τέτοιες παραγωγικές ανισότητες μπορούμε να προτείνουμε, για παράδειγμα, τα εξής: Συμπερασματικά, δίνουμε ένα παράδειγμα ενός συνόλου προβλημάτων για την επίλυση τριγωνομετρικών ανισώσεων. 1. Λύστε τις ανισώσεις: ΕΝΑ) σι) 5. Βρείτε όλες τις λύσεις στις ανισότητες: ΕΝΑ) ;
σι) ;
V) ΣΟΛ) ρε) 6. Λύστε τις ανισώσεις: ΕΝΑ) ;
σι) ;
V) ; ΣΟΛ) δ) ; ε) ; και) 7. Λύστε τις ανισώσεις: ΕΝΑ) σι) ;
V) ; Ζ) . 8. Λύστε τις ανισώσεις: ΕΝΑ) ;
σι) ;
V) ; ΣΟΛ) ρε) ε) ; και) η) . Συνιστάται να προσφέρετε τις εργασίες 6 και 7 σε μαθητές που σπουδάζουν μαθηματικά σε προχωρημένο επίπεδο, εργασία 8 σε μαθητές σε τάξεις με προχωρημένη μελέτη μαθηματικών. §3. Ειδικές μέθοδοι επίλυσης τριγωνομετρικών ανισώσεων
Ειδικές μέθοδοι επίλυσης τριγωνομετρικών εξισώσεων - δηλαδή εκείνες οι μέθοδοι που μπορούν να χρησιμοποιηθούν μόνο για την επίλυση τριγωνομετρικών εξισώσεων. Αυτές οι μέθοδοι βασίζονται στη χρήση των ιδιοτήτων των τριγωνομετρικών συναρτήσεων, καθώς και στη χρήση διαφόρων τριγωνομετρικών τύπων και ταυτοτήτων. 3.1. Τομεακή μέθοδος
Ας εξετάσουμε τη μέθοδο τομέα για την επίλυση τριγωνομετρικών ανισώσεων. Επίλυση ανισώσεων της μορφής Στη μέθοδο του διαστήματος, κάθε γραμμικός παράγοντας του αριθμητή και του παρονομαστή της φόρμας Πρέπει να θυμόμαστε τα ακόλουθα: α) Παράγοντες της μορφής β) Παράγοντες της μορφής Παράδειγμα 1.
Λύστε ανισότητες: α) 3.2. Μέθοδος ομόκεντρου κύκλου
Αυτή η μέθοδος είναι ένα ανάλογο της μεθόδου των αξόνων παράλληλων αριθμών για την επίλυση συστημάτων ορθολογικών ανισοτήτων. Ας εξετάσουμε ένα παράδειγμα συστήματος ανισοτήτων. Παράδειγμα 5.
Να λύσετε ένα σύστημα απλών τριγωνομετρικών ανισώσεων Αρχικά, λύνουμε κάθε ανισότητα ξεχωριστά (Εικόνα 5). Στην επάνω δεξιά γωνία του σχήματος θα δείξουμε για ποιο όρισμα εξετάζεται ο τριγωνομετρικός κύκλος. Εικ.5 Στη συνέχεια, χτίζουμε ένα σύστημα ομόκεντρων κύκλων για το επιχείρημαΧ
. Σχεδιάζουμε έναν κύκλο και τον σκιάζουμε σύμφωνα με τη λύση της πρώτης ανισότητας, μετά σχεδιάζουμε έναν κύκλο μεγαλύτερης ακτίνας και τον σκιάζουμε σύμφωνα με τη λύση της δεύτερης, μετά κατασκευάζουμε έναν κύκλο για την τρίτη ανισότητα και έναν κύκλο βάσης. Σχεδιάζουμε ακτίνες από το κέντρο του συστήματος μέσω των άκρων των τόξων έτσι ώστε να τέμνουν όλους τους κύκλους. Σχηματίζουμε ένα διάλυμα στον κύκλο της βάσης (Εικόνα 6). Εικ.6 Απάντηση:
Σύναψη
Όλοι οι στόχοι της έρευνας του μαθήματος ολοκληρώθηκαν. Το θεωρητικό υλικό συστηματοποιείται: δίνονται οι κύριοι τύποι τριγωνομετρικών ανισώσεων και οι κύριες μέθοδοι επίλυσής τους (γραφική, αλγεβρική, μέθοδος διαστημάτων, τομείς και μέθοδος ομόκεντρων κύκλων). Για κάθε μέθοδο δόθηκε ένα παράδειγμα επίλυσης ανισότητας. Το θεωρητικό μέρος ακολούθησε το πρακτικό. Περιέχει ένα σύνολο εργασιών για την επίλυση τριγωνομετρικών ανισώσεων. Αυτό το μάθημα μπορεί να χρησιμοποιηθεί από φοιτητές για ανεξάρτητη εργασία. Οι μαθητές μπορούν να ελέγξουν το επίπεδο γνώσης αυτού του θέματος και να εξασκηθούν στην ολοκλήρωση εργασιών διαφορετικής πολυπλοκότητας. Έχοντας μελετήσει τη σχετική βιβλιογραφία για αυτό το θέμα, μπορούμε προφανώς να συμπεράνουμε ότι η ικανότητα και οι δεξιότητες επίλυσης τριγωνομετρικών ανισοτήτων στο σχολικό μάθημα της άλγεβρας και της στοιχειώδους ανάλυσης είναι πολύ σημαντικές, η ανάπτυξη των οποίων απαιτεί σημαντική προσπάθεια από την πλευρά του δασκάλου των μαθηματικών. Ως εκ τούτου, αυτή η εργασία θα είναι χρήσιμη για τους καθηγητές μαθηματικών, καθώς καθιστά δυνατή την αποτελεσματική οργάνωση της εκπαίδευσης των μαθητών στο θέμα «Τριγωνομετρικές ανισότητες». Η έρευνα μπορεί να συνεχιστεί επεκτείνοντάς την σε μια τελική ειδική εργασία.
Κατάλογος χρησιμοποιημένης βιβλιογραφίας
Bogomolov, N.V. Συλλογή προβλημάτων στα μαθηματικά [Κείμενο] / N.V. Μπογκομόλοφ. – M.: Bustard, 2009. – 206 σελ. Vygodsky, M.Ya. Εγχειρίδιο στοιχειωδών μαθηματικών [Κείμενο] / M.Ya. Vygodsky. – Μ.: Bustard, 2006. – 509 σελ. Zhurbenko, L.N. Τα μαθηματικά σε παραδείγματα και προβλήματα [Κείμενο] / Λ.Ν. Ζουρμπένκο. – M.: Infra-M, 2009. – 373 p. Ιβάνοφ, Ο.Α. Μαθηματικά Δημοτικού για μαθητές, μαθητές και δασκάλους [Κείμενο] / Ο.Α. Ιβάνοφ. – Μ.: MTsNMO, 2009. – 384 σελ. Karp, A.P. Εργασίες για την άλγεβρα και τις απαρχές της ανάλυσης για την οργάνωση τελικής επανάληψης και πιστοποίησης στην τάξη 11 [Κείμενο] / Α.Π. Κυπρίνος. – Μ.: Εκπαίδευση, 2005. – 79 σελ. Kulanin, E.D. 3000 αγωνιστικά προβλήματα στα μαθηματικά [Κείμενο] / Ε.Δ. Κουλανίν. – Μ.: Iris-press, 2007. – 624 σελ. Leibson, K.L. Συλλογή πρακτικών εργασιών στα μαθηματικά [Κείμενο] / Κ.Λ. Leibson. – Μ.: Bustard, 2010. – 182 σελ. Elbow, V.V. Προβλήματα με τις παραμέτρους και τις λύσεις τους. Τριγωνομετρία: εξισώσεις, ανισώσεις, συστήματα. 10η τάξη [Κείμενο] / V.V. Αγκώνας. – Μ.: ΑΡΚΤΗ, 2008. – 64 σελ. Μάνοβα, Α.Ν. Μαθηματικά. Εξπρές δάσκαλος για την προετοιμασία για την Ενιαία Κρατική Εξέταση: φοιτητής. εγχειρίδιο [Κείμενο] / A.N. Μάνοβα. – Rostov-on-Don: Phoenix, 2012. – 541 p. Mordkovich, A.G. Άλγεβρα και οι απαρχές της μαθηματικής ανάλυσης. 10-11 τάξεις. Εγχειρίδιο για μαθητές γενικής εκπαίδευσης [Κείμενο] / Α.Γ. Μόρντκοβιτς. – Μ.: Iris-press, 2009. – 201 σελ. Novikov, A.I. Τριγωνομετρικές συναρτήσεις, εξισώσεις και ανισώσεις [Κείμενο] / A.I. Νοβίκοφ. – Μ.: FIZMATLIT, 2010. – 260 σελ. Oganesyan, V.A. Μέθοδοι διδασκαλίας των μαθηματικών στη δευτεροβάθμια εκπαίδευση: Γενική μεθοδολογία. Σχολικό βιβλίο εγχειρίδιο για φοιτητές φυσικής - χαλάκι. ψεύτικο. πεδ. Inst. [Κείμενο] / V.A. Oganesyan. – Μ.: Εκπαίδευση, 2006. – 368 σελ. Olehnik, S.N. Εξισώσεις και ανισώσεις. Μη τυπικές μέθοδοι λύσης [Κείμενο] / S.N. Olehnik. – M.: Factorial Publishing House, 1997. – 219 σελ. Sevryukov, P.F. Τριγωνομετρικές, εκθετικές και λογαριθμικές εξισώσεις και ανισώσεις [Κείμενο] / Π.Φ. Σεβριούκοφ. – Μ.: Δημόσια Εκπαίδευση, 2008. – 352 σελ. Σεργκέεφ, Ι.Ν. Ενιαία Κρατική Εξέταση: 1000 προβλήματα με απαντήσεις και λύσεις στα μαθηματικά. Όλες οι εργασίες της ομάδας Γ [Κείμενο] / Ι.Ν. Σεργκέεφ. – Μ.: Εξεταστική, 2012. – 301 σελ. Sobolev, A.B. Μαθηματικά Δημοτικού [Κείμενο] / Α.Β. Sobolev. – Ekaterinburg: State Educational Institution of Higher Professional Education USTU-UPI, 2005. – 81 p. Fenko, L.M. Μέθοδος διαστημάτων επίλυσης ανισώσεων και μελέτης συναρτήσεων [Κείμενο] / Λ.Μ. Φένκο. – M.: Bustard, 2005. – 124 σελ. Friedman, L.M. Θεωρητικές βάσεις μεθόδων διδασκαλίας των μαθηματικών [Κείμενο] / Λ.Μ. Ο Φρίντμαν. – Μ.: Βιβλιοθήκη “LIBROKOM”, 2009. – 248 σελ. Παράρτημα 1 Γραφική ερμηνεία λύσεων σε απλές ανισότητες Ρύζι. 1 Ρύζι. 2 Εικ.3 Εικ.4 Εικ.5 Εικ.6 Εικ.7 Εικ.8 Παράρτημα 2 Λύσεις σε απλές ανισότητες Ένας αλγόριθμος για την επίλυση απλών τριγωνομετρικών ανισώσεων και την αναγνώριση μεθόδων επίλυσης τριγωνομετρικών ανισώσεων. Δάσκαλοι της υψηλότερης κατηγορίας προσόντων: Shirko F.M. σ. Πρόοδος, MOBU-λυκείου Νο. 6 Sankina L.S. Armavir, ιδιωτικό γυμνάσιο "New Way" Δεν υπάρχουν καθολικές μέθοδοι διδασκαλίας επιστημονικών και μαθηματικών κλάδων. Κάθε δάσκαλος βρίσκει τους δικούς του τρόπους διδασκαλίας που είναι αποδεκτοί μόνο από αυτόν. Η πολυετής διδακτική μας εμπειρία δείχνει ότι οι μαθητές μαθαίνουν ευκολότερα υλικό που απαιτεί συγκέντρωση και διατήρηση μεγάλου όγκου πληροφοριών στη μνήμη, εάν διδαχθούν να χρησιμοποιούν αλγόριθμους στις δραστηριότητές τους στο αρχικό στάδιο της εκμάθησης ενός πολύπλοκου θέματος. Κατά τη γνώμη μας, ένα τέτοιο θέμα είναι το θέμα της επίλυσης τριγωνομετρικών ανισώσεων. Έτσι, πριν ξεκινήσουμε με τους μαθητές να εντοπίζουμε τεχνικές και μεθόδους για την επίλυση τριγωνομετρικών ανισώσεων, εξασκούμε και ενοποιούμε έναν αλγόριθμο για την επίλυση των απλούστερων τριγωνομετρικών ανισώσεων. Αλγόριθμος επίλυσης απλών τριγωνομετρικών ανισώσεων
Σημειώστε σημεία στον αντίστοιχο άξονα ( Για
αμαρτία
x– Άξονας ΟΑ, γιασυν
x– Άξονας OX) Επαναφέρουμε μια κάθετη στον άξονα που θα τέμνει τον κύκλο σε δύο σημεία. Το πρώτο σημείο στον κύκλο είναι ένα σημείο που ανήκει εξ ορισμού στο διάστημα του εύρους συναρτήσεων τόξου. Ξεκινώντας από το σημειωμένο σημείο, σκιάστε το τόξο του κύκλου που αντιστοιχεί στο σκιασμένο τμήμα του άξονα. Δίνουμε ιδιαίτερη προσοχή στην κατεύθυνση της παράκαμψης. Εάν η διέλευση γίνει δεξιόστροφα (δηλαδή υπάρχει μετάβαση στο 0), τότε το δεύτερο σημείο του κύκλου θα είναι αρνητικό, αν αριστερόστροφα θα είναι θετικό. Γράφουμε την απάντηση με τη μορφή διαστήματος, λαμβάνοντας υπόψη την περιοδικότητα της συνάρτησης. Ας δούμε τη λειτουργία του αλγορίθμου χρησιμοποιώντας παραδείγματα.
1)
αμαρτία
≥ 1/2;
Διάλυμα: Απεικονίζουμε έναν κύκλο μονάδας. Σημειώνουμε το σημείο ½ στον άξονα OU. Επαναφέρουμε την κάθετο στον άξονα, που τέμνει τον κύκλο σε δύο σημεία. Εξ ορισμού του τόξου, πρώτα σημειώνουμε σημείο π/6. Σκιάστε το τμήμα του άξονα που αντιστοιχεί δεδομένης ανισότητας, πάνω από το σημείο ½. Σκιάστε το τόξο του κύκλου που αντιστοιχεί στο σκιασμένο τμήμα του άξονα. Η διέλευση γίνεται αριστερόστροφα, παίρνουμε το σημείο 5π/6. Γράφουμε την απάντηση με τη μορφή ενός διαστήματος, λαμβάνοντας υπόψη την περιοδικότητα της συνάρτησης. Απάντηση:x;[π/6 + 2π n, 5π/6 + 2π n], n Ζ. Η απλούστερη ανισότητα λύνεται χρησιμοποιώντας τον ίδιο αλγόριθμο εάν η εγγραφή απάντησης δεν περιέχει τιμή πίνακα. Οι μαθητές, όταν λύνουν ανισότητες στον πίνακα στα πρώτα τους μαθήματα, απαγγέλλουν κάθε βήμα του αλγορίθμου δυνατά. 2) 5
συν
x
– 1 ≥ 0;
R 5 συν x – 1 ≥ 0; συν
x ≥ 1/5; Σχεδιάστε έναν κύκλο μονάδας. Σημειώνουμε ένα σημείο με συντεταγμένη 1/5 στον άξονα ΟΧ. Επαναφέρουμε την κάθετη στον άξονα, η οποία τέμνει τον κύκλο σε δύο σημεία. Το πρώτο σημείο του κύκλου είναι ένα σημείο που ανήκει εξ ορισμού στο διάστημα της περιοχής συνημιτόνου τόξου (0;π). Σκιάζουμε το τμήμα του άξονα που αντιστοιχεί σε αυτή την ανισότητα. Ξεκινώντας από το υπογεγραμμένο σημείο
τόξα 1/5, σκιάστε το τόξο του κύκλου που αντιστοιχεί στο σκιασμένο τμήμα του άξονα. Η διέλευση γίνεται δεξιόστροφα (δηλαδή υπάρχει μετάβαση στο 0), που σημαίνει ότι το δεύτερο σημείο στον κύκλο θα είναι αρνητικό - τόξα 1/5. Γράφουμε την απάντηση με τη μορφή διαστήματος, λαμβάνοντας υπόψη την περιοδικότητα της συνάρτησης, από τη μικρότερη τιμή στη μεγαλύτερη. Απάντηση: x [-τόξα 1/5 + 2π n, τόξα 1/5 + 2π n], n Ζ. Η βελτίωση της ικανότητας επίλυσης τριγωνομετρικών ανισώσεων διευκολύνεται από τις ακόλουθες ερωτήσεις: "Πώς θα λύσουμε μια ομάδα ανισώσεων;"; «Πώς διαφέρει μια ανισότητα από την άλλη;» "Πώς είναι μια ανισότητα παρόμοια με μια άλλη;"; Πώς θα άλλαζε η απάντηση αν δινόταν αυστηρή ανισότητα;" Πώς θα άλλαζε η απάντηση αν αντί για το σύμβολο "" υπήρχε ένα σημάδι " Η εργασία της ανάλυσης μιας λίστας ανισοτήτων από τη σκοπιά των μεθόδων επίλυσής τους σας επιτρέπει να εξασκήσετε την αναγνώρισή τους. Δίνονται στους μαθητές ανισότητες που πρέπει να λυθούν στην τάξη. Ερώτηση:Να επισημάνετε τις ανισότητες που απαιτούν τη χρήση ισοδύναμων μετασχηματισμών κατά την αναγωγή μιας τριγωνομετρικής ανισότητας στην απλούστερη μορφή της; Απάντηση 1, 3, 5. Ερώτηση:Ποιες είναι οι ανισότητες στις οποίες πρέπει να θεωρήσετε ένα σύνθετο επιχείρημα ως απλό; Απάντηση: 1, 2, 3, 5, 6. Ερώτηση:Ποιες είναι οι ανισότητες στις οποίες μπορούν να εφαρμοστούν τριγωνομετρικοί τύποι; Απάντηση: 2, 3, 6. Ερώτηση:Ονομάστε τις ανισότητες στις οποίες μπορεί να εφαρμοστεί η μέθοδος εισαγωγής μιας νέας μεταβλητής; Απάντηση: 6. Η εργασία της ανάλυσης μιας λίστας ανισοτήτων από τη σκοπιά των μεθόδων επίλυσής τους σας επιτρέπει να εξασκήσετε την αναγνώρισή τους. Κατά την ανάπτυξη δεξιοτήτων, είναι σημαντικό να προσδιορίσετε τα στάδια της εφαρμογής του και να τα διατυπώσετε σε μια γενική μορφή, η οποία παρουσιάζεται στον αλγόριθμο για την επίλυση των απλούστερων τριγωνομετρικών ανισοτήτων.Μέθοδος 1 - Επίλυση ανισώσεων με τη γραφική παράσταση μιας συνάρτησης
![]()
![]()
Μέθοδος 2 - Επίλυση τριγωνομετρικών ανισώσεων χρησιμοποιώντας τον μοναδιαίο κύκλο
![]()





Μιγαδικές τριγωνομετρικές ανισώσεις



Αλγόριθμος για την επίλυση ανισώσεων με ημίτονο:
Περιορισμός αλγορίθμου
Ειδικές περιπτώσεις κατά την επίλυση ανισώσεων με ημίτονο
Παραδείγματα επίλυσης ανισώσεων με χρήση αλγορίθμου.






 Άρα, η λύση σε αυτήν την ανισότητα θα είναι το διάστημα:
Άρα, η λύση σε αυτήν την ανισότητα θα είναι το διάστημα:
 ,
,  κ.λπ.), όπου πρώτα λύνεται η συνηθισμένη ανισότητα και μετά μια ανισότητα της μορφής
κ.λπ.), όπου πρώτα λύνεται η συνηθισμένη ανισότητα και μετά μια ανισότητα της μορφής  κ.λπ., ή άλλες μεθόδους.
κ.λπ., ή άλλες μεθόδους. αρκεί να βρεθεί η λύση του σε μια περίοδο, δηλ. σε οποιοδήποτε τμήμα του οποίου το μήκος είναι ίσο με την περίοδο της συνάρτησηςφά
x
. Τότε θα βρεθεί όλη η λύση στην αρχική ανισότηταx
, καθώς και εκείνες τις τιμές που διαφέρουν από αυτές που βρέθηκαν από οποιονδήποτε ακέραιο αριθμό περιόδων της συνάρτησης. Σε αυτή την περίπτωση, είναι βολικό να χρησιμοποιήσετε τη γραφική μέθοδο.
αρκεί να βρεθεί η λύση του σε μια περίοδο, δηλ. σε οποιοδήποτε τμήμα του οποίου το μήκος είναι ίσο με την περίοδο της συνάρτησηςφά
x
. Τότε θα βρεθεί όλη η λύση στην αρχική ανισότηταx
, καθώς και εκείνες τις τιμές που διαφέρουν από αυτές που βρέθηκαν από οποιονδήποτε ακέραιο αριθμό περιόδων της συνάρτησης. Σε αυτή την περίπτωση, είναι βολικό να χρησιμοποιήσετε τη γραφική μέθοδο. (
(
 ) Και
) Και  .
.
 (
(
 ).
).
 .
.
 .
.
 (ο αριθμός στα αριστερά της καταχώρισης είναι πάντα μικρότερος από τον αριθμό στα δεξιά).
(ο αριθμός στα αριστερά της καταχώρισης είναι πάντα μικρότερος από τον αριθμό στα δεξιά). .
.
 , που τέμνει τον κύκλο στα σημεία Α και Β.
, που τέμνει τον κύκλο στα σημεία Α και Β. , αλλά μικρότερο
, αλλά μικρότερο  ,
,
 θα πάρει αξίες μεγαλύτερες
(αλλά όχι περισσότερα από ένα).
θα πάρει αξίες μεγαλύτερες
(αλλά όχι περισσότερα από ένα).
 , δηλ.
, δηλ.  . Για να ληφθούν όλες οι λύσεις σε αυτήν την ανισότητα, αρκεί να προσθέσουμε στα άκρα αυτού του διαστήματος
. Για να ληφθούν όλες οι λύσεις σε αυτήν την ανισότητα, αρκεί να προσθέσουμε στα άκρα αυτού του διαστήματος  , Πού
, Πού  , δηλ.
, δηλ.  ,
,
 .
Σημειώστε ότι οι τιμές
.
Σημειώστε ότι οι τιμές  Και
Και  είναι οι ρίζες της εξίσωσης
είναι οι ρίζες της εξίσωσης  ,
,
 ;
;
 .
.
 ,
,  .
.
 :
:
 Και
Και  .
.
 . Βρίσκουμε τα τετμημένα αυτών των σημείων.
. Βρίσκουμε τα τετμημένα αυτών των σημείων.
 Και
Και  (Εικ. 2).
(Εικ. 2).
 ;
;  . Ανάμεσος
. Ανάμεσος  σημεία γραφήματος
σημεία γραφήματος  κάτω από τα σημεία του γραφήματος
κάτω από τα σημεία του γραφήματος  . Και πότε
. Και πότε  οι τιμές των συναρτήσεων είναι ίδιες. Γι' αυτό
οι τιμές των συναρτήσεων είναι ίδιες. Γι' αυτό  στο
στο  .
.
 .
.
 .
.

 (Εικ. 3)
(Εικ. 3)

 ,
,  .
.

 ,
, 
 ,
,  .
.
 ,
, 
 .
.
 μετά από απλούς μετασχηματισμούς παίρνουμε
μετά από απλούς μετασχηματισμούς παίρνουμε ,
,
 ,
,
 .
.

 , αντίστοιχα
, αντίστοιχα  . Στη συνέχεια από το Σχ. 4 ακολουθεί
. Στη συνέχεια από το Σχ. 4 ακολουθεί  , Πού
, Πού  .
.

 ,
,  .
.
 ,
,  .
.
 .
.
 .
.
 : . Ας σημειώσουμε όλα τα σημεία στον μοναδιαίο κύκλο (Εικ. 6):
: . Ας σημειώσουμε όλα τα σημεία στον μοναδιαίο κύκλο (Εικ. 6):
 ,
,  ;
;  ,
,  ;
;  ,
,  .
.
 ,
,
 ;
;
 ,
,  ;
;
 ,
,  ;
;
 ,
,  ;
;
 . ΣειράΧ
2
δίνει πόντους
. ΣειράΧ
2
δίνει πόντους  . Από τη σειράΧ
3
παίρνουμε δύο βαθμούς
. Από τη σειράΧ
3
παίρνουμε δύο βαθμούς  . Τέλος, η σειράΧ
4
θα αντιπροσωπεύει σημεία
. Τέλος, η σειράΧ
4
θα αντιπροσωπεύει σημεία  . Ας σχεδιάσουμε όλα αυτά τα σημεία στον μοναδιαίο κύκλο, υποδεικνύοντας την πολλαπλότητα του σε παρενθέσεις δίπλα σε καθένα από αυτά.
. Ας σχεδιάσουμε όλα αυτά τα σημεία στον μοναδιαίο κύκλο, υποδεικνύοντας την πολλαπλότητα του σε παρενθέσεις δίπλα σε καθένα από αυτά. θα είναι ίσοι. Ας κάνουμε μια εκτίμηση με βάση το πρόσημο:
θα είναι ίσοι. Ας κάνουμε μια εκτίμηση με βάση το πρόσημο:
 με δοκάριΩ,
έξω από τον κύκλο της μονάδας. (Σημειώστε ότι η βοηθητική δοκόςΓΙΑ
ΕΝΑ
Δεν είναι καθόλου απαραίτητο να το απεικονίσετε σε σχέδιο. ΤελείαΕΝΑ
επιλέγεται κατά προσέγγιση.)
με δοκάριΩ,
έξω από τον κύκλο της μονάδας. (Σημειώστε ότι η βοηθητική δοκόςΓΙΑ
ΕΝΑ
Δεν είναι καθόλου απαραίτητο να το απεικονίσετε σε σχέδιο. ΤελείαΕΝΑ
επιλέγεται κατά προσέγγιση.) Η γραμμή μας πηγαίνει από τη μια περιοχή στην άλλη: αν ήταν εκτός του κύκλου της μονάδας, τότε πηγαίνει μέσα σε αυτήν. Πλησιάζοντας το σημείο
Η γραμμή μας πηγαίνει από τη μια περιοχή στην άλλη: αν ήταν εκτός του κύκλου της μονάδας, τότε πηγαίνει μέσα σε αυτήν. Πλησιάζοντας το σημείο  , η γραμμή επιστρέφει στην εσωτερική περιοχή, αφού η πολλαπλότητα αυτού του σημείου είναι άρτια. Ομοίως στο σημείο
, η γραμμή επιστρέφει στην εσωτερική περιοχή, αφού η πολλαπλότητα αυτού του σημείου είναι άρτια. Ομοίως στο σημείο  (με άρτια πολλαπλότητα) η γραμμή πρέπει να στραφεί προς την εξωτερική περιοχή. Έτσι, σχεδιάσαμε μια συγκεκριμένη εικόνα που φαίνεται στο Σχ. 7. Βοηθά στην επισήμανση των επιθυμητών περιοχών στον κύκλο της μονάδας. Σημειώνονται με το σύμβολο «+».
(με άρτια πολλαπλότητα) η γραμμή πρέπει να στραφεί προς την εξωτερική περιοχή. Έτσι, σχεδιάσαμε μια συγκεκριμένη εικόνα που φαίνεται στο Σχ. 7. Βοηθά στην επισήμανση των επιθυμητών περιοχών στον κύκλο της μονάδας. Σημειώνονται με το σύμβολο «+».
 ,
,
 ,
,  ,
,
 ,
χρησιμοποιώντας τις ιδιότητες των συναρτήσεων ημιτονοειδούς και συνημιτονοειδούς.
,
χρησιμοποιώντας τις ιδιότητες των συναρτήσεων ημιτονοειδούς και συνημιτονοειδούς. , Αν
, Αν , Αν
, Αν  ισούται με:
ισούται με: 
 , Εάν:
, Εάν:
 ,
σι)
,
σι)  ,
V)
,
V) 

 ,
,  ,
,  ,
,  .
.
 .
Χρησιμοποιώντας τις γνώσεις και τις δεξιότητες που αποκτήθηκαν στο προπαρασκευαστικό στάδιο, οι μαθητές θα φέρουν την προτεινόμενη ανισότητα στη μορφή
.
Χρησιμοποιώντας τις γνώσεις και τις δεξιότητες που αποκτήθηκαν στο προπαρασκευαστικό στάδιο, οι μαθητές θα φέρουν την προτεινόμενη ανισότητα στη μορφή  , αλλά μπορεί να δυσκολεύεται να βρει ένα σύνολο λύσεων για την προκύπτουσα ανισότητα, επειδή Είναι αδύνατο να λυθεί μόνο χρησιμοποιώντας τις ιδιότητες της συνάρτησης ημιτόνου. Αυτή η δυσκολία μπορεί να αποφευχθεί στρέφοντας στην κατάλληλη απεικόνιση (λύνοντας την εξίσωση γραφικά ή χρησιμοποιώντας έναν κύκλο μονάδας).
, αλλά μπορεί να δυσκολεύεται να βρει ένα σύνολο λύσεων για την προκύπτουσα ανισότητα, επειδή Είναι αδύνατο να λυθεί μόνο χρησιμοποιώντας τις ιδιότητες της συνάρτησης ημιτόνου. Αυτή η δυσκολία μπορεί να αποφευχθεί στρέφοντας στην κατάλληλη απεικόνιση (λύνοντας την εξίσωση γραφικά ή χρησιμοποιώντας έναν κύκλο μονάδας). .
.
 και τραβήξτε μια ευθεία μέσα από αυτήν παράλληλη προς τον άξονα x. Αυτή η ευθεία θα τέμνει τον μοναδιαίο κύκλο σε δύο σημεία. Κάθε ένα από αυτά τα σημεία αντιπροσωπεύει αριθμούς των οποίων το ημίτονο είναι ίσο με
και τραβήξτε μια ευθεία μέσα από αυτήν παράλληλη προς τον άξονα x. Αυτή η ευθεία θα τέμνει τον μοναδιαίο κύκλο σε δύο σημεία. Κάθε ένα από αυτά τα σημεία αντιπροσωπεύει αριθμούς των οποίων το ημίτονο είναι ίσο με  .
.
 . Φυσικά, αυτό το τόξο βρίσκεται πάνω από την τραβηγμένη ευθεία γραμμή.
. Φυσικά, αυτό το τόξο βρίσκεται πάνω από την τραβηγμένη ευθεία γραμμή.
 .
.
 .
.
 ικανοποιήστε τους αριθμούς για τους οποίους ισχύει η ανισότητα
ικανοποιήστε τους αριθμούς για τους οποίους ισχύει η ανισότητα  . Επιλύσαμε την ανίσωση για αριθμούς που βρίσκονται στην ίδια περίοδο της ημιτονοειδούς συνάρτησης. Επομένως, όλες οι λύσεις στην ανισότητα μπορούν να γραφτούν με τη μορφή
. Επιλύσαμε την ανίσωση για αριθμούς που βρίσκονται στην ίδια περίοδο της ημιτονοειδούς συνάρτησης. Επομένως, όλες οι λύσεις στην ανισότητα μπορούν να γραφτούν με τη μορφή ![]()
 μπορεί να γραφτεί στη φόρμα
μπορεί να γραφτεί στη φόρμα  ,
,  .
.

 Και
Και  , δεδομένου ότι
, δεδομένου ότι  .
.

 και την απόφασή του
και την απόφασή του  ,
,  ,
,  , βρέθηκε χρησιμοποιώντας τύπους
, βρέθηκε χρησιμοποιώντας τύπους  ,
,  ,
,  .
.
 είναι τρεις διαδοχικές τετμημένες των σημείων τομής των γραφημάτων
είναι τρεις διαδοχικές τετμημένες των σημείων τομής των γραφημάτων  Και
Και  . Προφανώς, πάντα στο μεσοδιάστημα
. Προφανώς, πάντα στο μεσοδιάστημα  η ανισότητα ισχύει
η ανισότητα ισχύει  , και στο μεσοδιάστημα
, και στο μεσοδιάστημα  – ανισότητα
– ανισότητα  . Μας ενδιαφέρει η πρώτη περίπτωση και μετά προσθέτοντας στα άκρα αυτού του διαστήματος έναν αριθμό που είναι πολλαπλάσιο της περιόδου του ημιτονοειδούς, παίρνουμε μια λύση στην ανισότητα
. Μας ενδιαφέρει η πρώτη περίπτωση και μετά προσθέτοντας στα άκρα αυτού του διαστήματος έναν αριθμό που είναι πολλαπλάσιο της περιόδου του ημιτονοειδούς, παίρνουμε μια λύση στην ανισότητα  με τη μορφή:
με τη μορφή:  ,
,  .
.

 , πρέπει να δημιουργήσετε την αντίστοιχη εξίσωση και να τη λύσετε. Βρείτε τις ρίζες από τον τύπο που προκύπτει
, πρέπει να δημιουργήσετε την αντίστοιχη εξίσωση και να τη λύσετε. Βρείτε τις ρίζες από τον τύπο που προκύπτει  Και
Και  και γράψτε την απάντηση στην ανισότητα με τη μορφή: ,
και γράψτε την απάντηση στην ανισότητα με τη μορφή: ,  .
.


![]()
![]()
 , ικανοποιώντας την προϋπόθεση
, ικανοποιώντας την προϋπόθεση  ;
;
 , ικανοποιώντας την προϋπόθεση
, ικανοποιώντας την προϋπόθεση  .
.
 ;
;
 ;
;
 .
.
 ;
;
 .
.
 ;
;
 ;
;
 ;
;
 ;
;

 , ΠούΠ
(
x
)
ΚαιQ
(
x
)
– ορθολογικές τριγωνομετρικές συναρτήσεις (οι ημίτονο, συνημίτονο, εφαπτομένες και συνεφαπτομένες περιλαμβάνονται σε αυτές ορθολογικά), παρόμοιες με την επίλυση ορθολογικών ανισοτήτων. Είναι βολικό να λύνουμε ορθολογικές ανισότητες χρησιμοποιώντας τη μέθοδο των διαστημάτων στην αριθμητική γραμμή. Το ανάλογό του για την επίλυση ορθολογικών τριγωνομετρικών ανισώσεων είναι η μέθοδος των τομέων στον τριγωνομετρικό κύκλο, γιαsinx
Καιcosx
(
, ΠούΠ
(
x
)
ΚαιQ
(
x
)
– ορθολογικές τριγωνομετρικές συναρτήσεις (οι ημίτονο, συνημίτονο, εφαπτομένες και συνεφαπτομένες περιλαμβάνονται σε αυτές ορθολογικά), παρόμοιες με την επίλυση ορθολογικών ανισοτήτων. Είναι βολικό να λύνουμε ορθολογικές ανισότητες χρησιμοποιώντας τη μέθοδο των διαστημάτων στην αριθμητική γραμμή. Το ανάλογό του για την επίλυση ορθολογικών τριγωνομετρικών ανισώσεων είναι η μέθοδος των τομέων στον τριγωνομετρικό κύκλο, γιαsinx
Καιcosx
( ) ή τριγωνομετρικό ημικύκλιο γιαtgx
Καιctgx
(
) ή τριγωνομετρικό ημικύκλιο γιαtgx
Καιctgx
(
 ).
).
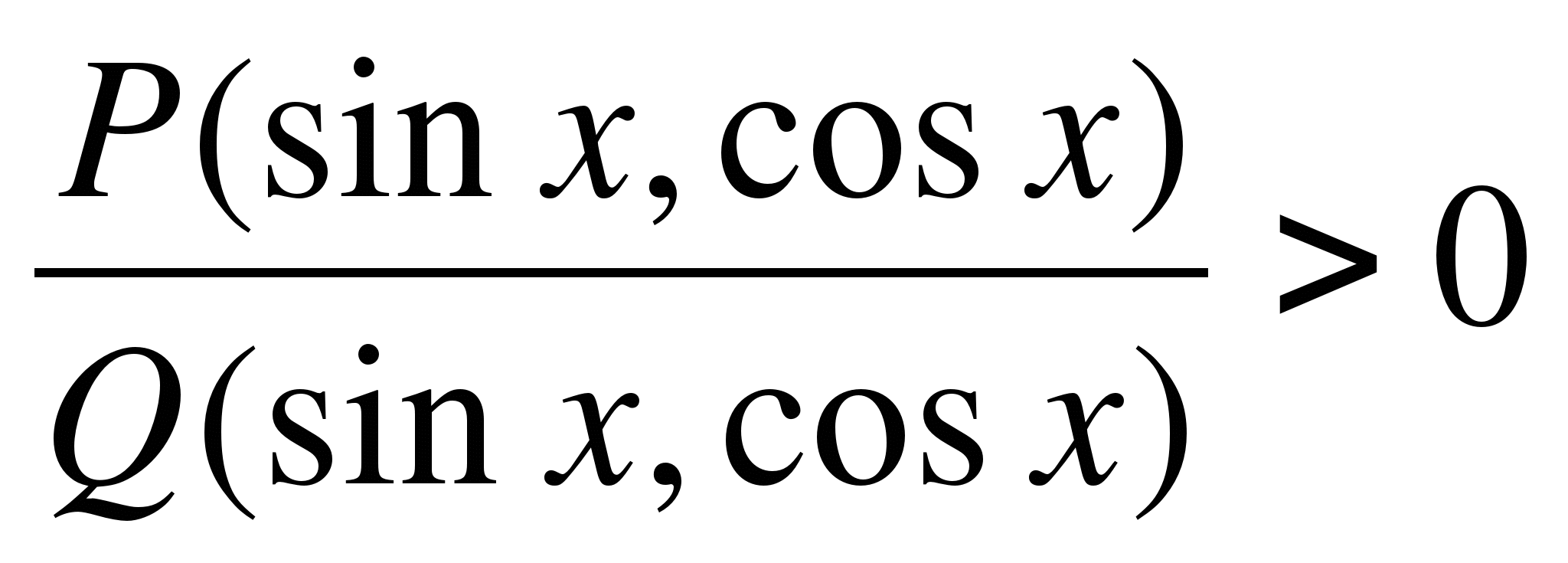
 στον αριθμητικό άξονα αντιστοιχεί σε ένα σημείο
στον αριθμητικό άξονα αντιστοιχεί σε ένα σημείο  , και κατά τη διέλευση από αυτό το σημείο
, και κατά τη διέλευση από αυτό το σημείο  αλλάζει σημάδι. Στη μέθοδο τομέα, κάθε παράγοντας της φόρμας
αλλάζει σημάδι. Στη μέθοδο τομέα, κάθε παράγοντας της φόρμας  , Πού
, Πού  - μία από τις λειτουργίεςsinx
ήcosx
Και
- μία από τις λειτουργίεςsinx
ήcosx
Και  , σε τριγωνομετρικό κύκλο αντιστοιχούν δύο γωνίες
, σε τριγωνομετρικό κύκλο αντιστοιχούν δύο γωνίες  Και
Και 
 , που χωρίζουν τον κύκλο σε δύο τομείς. Όταν διέρχεται από
, που χωρίζουν τον κύκλο σε δύο τομείς. Όταν διέρχεται από  Και
Και  λειτουργία
λειτουργία  αλλάζει σημάδι.
αλλάζει σημάδι. Και
Και  , Πού
, Πού  , διατηρήστε το σύμβολο για όλες τις τιμές
, διατηρήστε το σύμβολο για όλες τις τιμές  . Τέτοιοι παράγοντες του αριθμητή και του παρονομαστή απορρίπτονται αλλάζοντας (αν
. Τέτοιοι παράγοντες του αριθμητή και του παρονομαστή απορρίπτονται αλλάζοντας (αν  ) με κάθε τέτοια απόρριψη, το πρόσημο της ανισότητας αντιστρέφεται.
) με κάθε τέτοια απόρριψη, το πρόσημο της ανισότητας αντιστρέφεται. Και
Και  απορρίπτονται επίσης. Επιπλέον, εάν πρόκειται για συντελεστές του παρονομαστή, τότε οι ανισότητες της μορφής προστίθενται στο ισοδύναμο σύστημα ανισώσεων
απορρίπτονται επίσης. Επιπλέον, εάν πρόκειται για συντελεστές του παρονομαστή, τότε οι ανισότητες της μορφής προστίθενται στο ισοδύναμο σύστημα ανισώσεων  Και
Και  . Εάν πρόκειται για συντελεστές του αριθμητή, τότε στο ισοδύναμο σύστημα περιορισμών αντιστοιχούν στις ανισότητες
. Εάν πρόκειται για συντελεστές του αριθμητή, τότε στο ισοδύναμο σύστημα περιορισμών αντιστοιχούν στις ανισότητες  Και
Και  σε περίπτωση αυστηρής αρχικής ανισότητας και ισότητας
σε περίπτωση αυστηρής αρχικής ανισότητας και ισότητας  Και
Και  στην περίπτωση μιας μη αυστηρής αρχικής ανισότητας. Κατά την απόρριψη του πολλαπλασιαστή
στην περίπτωση μιας μη αυστηρής αρχικής ανισότητας. Κατά την απόρριψη του πολλαπλασιαστή  ή
ή  το πρόσημο της ανισότητας αντιστρέφεται.
το πρόσημο της ανισότητας αντιστρέφεται. , β)
, β)  .
έχουμε συνάρτηση β) . Λύστε την ανισότητα που έχουμε,
.
έχουμε συνάρτηση β) . Λύστε την ανισότητα που έχουμε,


 ,
,  .
.














 διάλυμα:στο
διάλυμα:στο





