Η διατήρηση του απορρήτου σας είναι σημαντική για εμάς. Για το λόγο αυτό, έχουμε αναπτύξει μια Πολιτική Απορρήτου που περιγράφει τον τρόπο με τον οποίο χρησιμοποιούμε και αποθηκεύουμε τις πληροφορίες σας. Διαβάστε τις πρακτικές απορρήτου μας και ενημερώστε μας εάν έχετε ερωτήσεις.
Συλλογή και χρήση προσωπικών πληροφοριών
Οι προσωπικές πληροφορίες αναφέρονται σε δεδομένα που μπορούν να χρησιμοποιηθούν για την ταυτοποίηση συγκεκριμένο άτομοή επικοινωνήστε μαζί του.
Ενδέχεται να σας ζητηθεί να δώσετε τα προσωπικά σας στοιχεία ανά πάσα στιγμή όταν επικοινωνήσετε μαζί μας.
Ακολουθούν ορισμένα παραδείγματα των τύπων προσωπικών πληροφοριών που ενδέχεται να συλλέγουμε και πώς μπορούμε να χρησιμοποιήσουμε αυτές τις πληροφορίες.
Ποιες προσωπικές πληροφορίες συλλέγουμε:
- Όταν υποβάλλετε μια αίτηση στον ιστότοπο, ενδέχεται να συλλέξουμε διάφορες πληροφορίες, όπως το όνομά σας, τον αριθμό τηλεφώνου, τη διεύθυνσή σας e-mailκαι τα λοιπά.
Πώς χρησιμοποιούμε τα προσωπικά σας στοιχεία:
- Συλλέγεται από εμάς προσωπικές πληροφορίεςμας επιτρέπει να επικοινωνήσουμε μαζί σας και να σας ενημερώσουμε για μοναδικές προσφορές, προσφορές και άλλες εκδηλώσεις και επερχόμενες εκδηλώσεις.
- Από καιρό σε καιρό, ενδέχεται να χρησιμοποιήσουμε τα προσωπικά σας στοιχεία για να στείλουμε σημαντικές ειδοποιήσεις και επικοινωνίες.
- Ενδέχεται επίσης να χρησιμοποιήσουμε προσωπικές πληροφορίες για εσωτερικούς σκοπούς, όπως διεξαγωγή ελέγχων, ανάλυση δεδομένων και διάφορες έρευνες, προκειμένου να βελτιώσουμε τις υπηρεσίες που παρέχουμε και να σας παρέχουμε συστάσεις σχετικά με τις υπηρεσίες μας.
- Εάν συμμετέχετε σε κλήρωση, διαγωνισμό ή παρόμοια προσφορά, ενδέχεται να χρησιμοποιήσουμε τις πληροφορίες που παρέχετε για τη διαχείριση τέτοιων προγραμμάτων.
Αποκάλυψη πληροφοριών σε τρίτους
Δεν αποκαλύπτουμε τις πληροφορίες που λαμβάνουμε από εσάς σε τρίτους.
Εξαιρέσεις:
- Εάν είναι απαραίτητο - σύμφωνα με το νόμο, τη δικαστική διαδικασία, τις νομικές διαδικασίες ή/και με βάση δημόσια αιτήματα ή αιτήματα από κρατικούς φορείςστο έδαφος της Ρωσικής Ομοσπονδίας - αποκαλύψτε τα προσωπικά σας στοιχεία. Ενδέχεται επίσης να αποκαλύψουμε πληροφορίες σχετικά με εσάς εάν κρίνουμε ότι αυτή η αποκάλυψη είναι απαραίτητη ή κατάλληλη για λόγους ασφάλειας, επιβολής του νόμου ή άλλους σκοπούς δημόσιας σημασίας.
- Σε περίπτωση αναδιοργάνωσης, συγχώνευσης ή πώλησης, ενδέχεται να μεταφέρουμε τις προσωπικές πληροφορίες που συλλέγουμε στον αντίστοιχο τρίτο διάδοχο.
Προστασία προσωπικών πληροφοριών
Λαμβάνουμε προφυλάξεις - συμπεριλαμβανομένων διοικητικών, τεχνικών και φυσικών - για την προστασία των προσωπικών σας δεδομένων από απώλεια, κλοπή και κακή χρήση, καθώς και από μη εξουσιοδοτημένη πρόσβαση, αποκάλυψη, τροποποίηση και καταστροφή.
Σεβασμός του απορρήτου σας σε εταιρικό επίπεδο
Για να διασφαλίσουμε ότι τα προσωπικά σας στοιχεία είναι ασφαλή, κοινοποιούμε τα πρότυπα απορρήτου και ασφάλειας στους υπαλλήλους μας και εφαρμόζουμε αυστηρά τις πρακτικές απορρήτου.
Η διατήρηση του απορρήτου σας είναι σημαντική για εμάς. Για το λόγο αυτό, έχουμε αναπτύξει μια Πολιτική Απορρήτου που περιγράφει τον τρόπο με τον οποίο χρησιμοποιούμε και αποθηκεύουμε τις πληροφορίες σας. Διαβάστε τις πρακτικές απορρήτου μας και ενημερώστε μας εάν έχετε ερωτήσεις.
Συλλογή και χρήση προσωπικών πληροφοριών
Οι προσωπικές πληροφορίες αναφέρονται σε δεδομένα που μπορούν να χρησιμοποιηθούν για την αναγνώριση ή επικοινωνία με ένα συγκεκριμένο άτομο.
Ενδέχεται να σας ζητηθεί να δώσετε τα προσωπικά σας στοιχεία ανά πάσα στιγμή όταν επικοινωνήσετε μαζί μας.
Ακολουθούν ορισμένα παραδείγματα των τύπων προσωπικών πληροφοριών που ενδέχεται να συλλέγουμε και πώς μπορούμε να χρησιμοποιήσουμε αυτές τις πληροφορίες.
Ποιες προσωπικές πληροφορίες συλλέγουμε:
- Όταν υποβάλλετε μια αίτηση στον ιστότοπο, ενδέχεται να συλλέξουμε διάφορες πληροφορίες, όπως το όνομά σας, τον αριθμό τηλεφώνου, τη διεύθυνση email σας κ.λπ.
Πώς χρησιμοποιούμε τα προσωπικά σας στοιχεία:
- Οι προσωπικές πληροφορίες που συλλέγουμε μας επιτρέπουν να επικοινωνήσουμε μαζί σας με μοναδικές προσφορές, προσφορές και άλλες εκδηλώσεις και επερχόμενες εκδηλώσεις.
- Από καιρό σε καιρό, ενδέχεται να χρησιμοποιήσουμε τα προσωπικά σας στοιχεία για να στείλουμε σημαντικές ειδοποιήσεις και επικοινωνίες.
- Ενδέχεται επίσης να χρησιμοποιήσουμε προσωπικές πληροφορίες για εσωτερικούς σκοπούς, όπως διεξαγωγή ελέγχων, ανάλυση δεδομένων και διάφορες έρευνες, προκειμένου να βελτιώσουμε τις υπηρεσίες που παρέχουμε και να σας παρέχουμε συστάσεις σχετικά με τις υπηρεσίες μας.
- Εάν συμμετέχετε σε κλήρωση, διαγωνισμό ή παρόμοια προσφορά, ενδέχεται να χρησιμοποιήσουμε τις πληροφορίες που παρέχετε για τη διαχείριση τέτοιων προγραμμάτων.
Αποκάλυψη πληροφοριών σε τρίτους
Δεν αποκαλύπτουμε τις πληροφορίες που λαμβάνουμε από εσάς σε τρίτους.
Εξαιρέσεις:
- Εάν είναι απαραίτητο - σύμφωνα με το νόμο, τη δικαστική διαδικασία, σε νομικές διαδικασίες και/ή βάσει δημόσιων αιτημάτων ή αιτημάτων από κυβερνητικές αρχές στην επικράτεια της Ρωσικής Ομοσπονδίας - να αποκαλύψετε τα προσωπικά σας στοιχεία. Ενδέχεται επίσης να αποκαλύψουμε πληροφορίες σχετικά με εσάς εάν κρίνουμε ότι αυτή η αποκάλυψη είναι απαραίτητη ή κατάλληλη για λόγους ασφάλειας, επιβολής του νόμου ή άλλους σκοπούς δημόσιας σημασίας.
- Σε περίπτωση αναδιοργάνωσης, συγχώνευσης ή πώλησης, ενδέχεται να μεταφέρουμε τις προσωπικές πληροφορίες που συλλέγουμε στον αντίστοιχο τρίτο διάδοχο.
Προστασία προσωπικών πληροφοριών
Λαμβάνουμε προφυλάξεις - συμπεριλαμβανομένων διοικητικών, τεχνικών και φυσικών - για την προστασία των προσωπικών σας δεδομένων από απώλεια, κλοπή και κακή χρήση, καθώς και από μη εξουσιοδοτημένη πρόσβαση, αποκάλυψη, τροποποίηση και καταστροφή.
Σεβασμός του απορρήτου σας σε εταιρικό επίπεδο
Για να διασφαλίσουμε ότι τα προσωπικά σας στοιχεία είναι ασφαλή, κοινοποιούμε τα πρότυπα απορρήτου και ασφάλειας στους υπαλλήλους μας και εφαρμόζουμε αυστηρά τις πρακτικές απορρήτου.
Κατόπιν αιτήματός σας!
13. Λύστε την εξίσωση 3-4cos 2 x=0. Να βρείτε το άθροισμα των ριζών του που ανήκουν στο διάστημα .
Ας μειώσουμε τον βαθμό του συνημιτόνου χρησιμοποιώντας τον τύπο: 1+cos2α=2cos 2 α. Παίρνουμε μια ισοδύναμη εξίσωση:
3-2(1+cos2x)=0 ⇒ 3-2-2cos2x=0 ⇒ -2cos2x=-1. Διαιρούμε και τις δύο πλευρές της ισότητας με (-2) και παίρνουμε την απλούστερη τριγωνομετρική εξίσωση:

14. Βρείτε το β 5 γεωμετρική πρόοδος, αν b 4 =25 και b 6 =16.
Κάθε όρος της γεωμετρικής προόδου, ξεκινώντας από τον δεύτερο, ισούται με τον αριθμητικό μέσο όρο των γειτονικών του όρων:
(b n) 2 =b n-1 ∙b n+1 . Έχουμε (b 5) 2 =b 4 ∙b 6 ⇒ (b 5) 2 =25·16 ⇒ b 5 =±5·4 ⇒ b 5 =±20.
15. Να βρείτε την παράγωγο της συνάρτησης: f(x)=tgx-ctgx.

16. Βρείτε το μεγαλύτερο και μικρότερη τιμήσυναρτήσεις y(x)=x 2 -12x+27
στο τμήμα.
Για να βρείτε τις μεγαλύτερες και τις μικρότερες τιμές μιας συνάρτησης y=f(x) στο τμήμα, πρέπει να βρείτε τις τιμές αυτής της συνάρτησης στα άκρα του τμήματος και σε εκείνα τα κρίσιμα σημεία που ανήκουν σε αυτό το τμήμα και, στη συνέχεια, να επιλέξετε τη μεγαλύτερη και τη μικρότερη από όλες τις λαμβανόμενες τιμές.
Ας βρούμε τις τιμές της συνάρτησης στο x=3 και στο x=7, δηλ. στα άκρα του τμήματος.
y(3)=3 2 -12∙3+27 =9-36+27=0;
y(7)=7 2 -12∙7+27 =49-84+27=-84+76=-8.
Να βρείτε την παράγωγο αυτής της συνάρτησης: y’(x)=(x 2 -12x+27)’ =2x-12=2(x-6); το κρίσιμο σημείο x=6 ανήκει σε αυτό το διάστημα. Ας βρούμε την τιμή της συνάρτησης στο x=6.
y(6)=6 2 -12∙6+27 =36-72+27=-72+63=-9. Τώρα επιλέγουμε από τις τρεις λαμβανόμενες τιμές: 0; -8 και -9 μεγαλύτερο και μικρότερο: στο μεγαλύτερο. =0; στο όνομα =-9.
17. Εύρημα γενική άποψηαντιπαράγωγα για τη συνάρτηση:
Αυτό το διάστημα είναι το πεδίο ορισμού αυτής της συνάρτησης. Οι απαντήσεις πρέπει να ξεκινούν με F(x) και όχι με f(x) - στο κάτω κάτω, ψάχνουμε για ένα αντιπαράγωγο. Εξ ορισμού, η συνάρτηση F(x) είναι αντιπαράγωγος της συνάρτησης f(x) αν ισχύει η ισότητα: F’(x)=f(x). Έτσι, μπορείτε απλά να βρείτε παράγωγα των προτεινόμενων απαντήσεων μέχρι να λάβετε τη δεδομένη συνάρτηση. Μια αυστηρή λύση είναι ο υπολογισμός του ολοκληρώματος μιας δεδομένης συνάρτησης. Εφαρμόζουμε τους τύπους:

19. Γράψτε μια εξίσωση για την ευθεία που περιέχει τη διάμεσο BD του τριγώνου ABC αν οι κορυφές του είναι A(-6; 2), B(6; 6) C(2; -6).
Για να συντάξετε την εξίσωση μιας ευθείας, πρέπει να γνωρίζετε τις συντεταγμένες 2 σημείων αυτής της ευθείας, αλλά γνωρίζουμε μόνο τις συντεταγμένες του σημείου Β. Εφόσον η διάμεσος BD διαιρεί την απέναντι πλευρά στο μισό, το σημείο D είναι το μέσο του τμήματος AC. Οι συντεταγμένες του μέσου ενός τμήματος είναι τα μισά αθροίσματα των αντίστοιχων συντεταγμένων των άκρων του τμήματος. Ας βρούμε τις συντεταγμένες του σημείου Δ.

20. Υπολογίζω:

24. Το εμβαδόν ενός κανονικού τριγώνου που βρίσκεται στη βάση ενός ορθού πρίσματος είναι ίσο με
Αυτό το πρόβλημα είναι το αντίστροφο του προβλήματος Νο. 24 από την επιλογή 0021.

25. Βρείτε το μοτίβο και εισάγετε τον αριθμό που λείπει: 1; 4; 9; 16; ...
Προφανώς αυτός ο αριθμός 25 , αφού μας δίνεται μια ακολουθία τετραγώνων φυσικών αριθμών:
1 2 ; 2 2 ; 3 2 ; 4 2 ; 5 2 ; …
Καλή τύχη και επιτυχία σε όλους!
Για να λυθεί με επιτυχία τριγωνομετρικές εξισώσειςβολικό στη χρήση μέθοδος μείωσηςσε προβλήματα που είχαν λυθεί προηγουμένως. Ας καταλάβουμε ποια είναι η ουσία αυτής της μεθόδου;
Σε οποιοδήποτε προτεινόμενο πρόβλημα, πρέπει να δείτε ένα πρόβλημα που λύθηκε προηγουμένως και, στη συνέχεια, χρησιμοποιώντας διαδοχικούς ισοδύναμους μετασχηματισμούς, προσπαθήστε να μειώσετε το πρόβλημα που σας δόθηκε σε ένα απλούστερο.
Έτσι, όταν λύνουν τριγωνομετρικές εξισώσεις, συνήθως δημιουργούν μια ορισμένη πεπερασμένη ακολουθία ισοδύναμων εξισώσεων, ο τελευταίος σύνδεσμος της οποίας είναι μια εξίσωση με προφανή λύση. Είναι σημαντικό μόνο να θυμόμαστε ότι εάν δεν αναπτυχθούν οι δεξιότητες για την επίλυση των απλούστερων τριγωνομετρικών εξισώσεων, τότε η επίλυση πιο σύνθετων εξισώσεων θα είναι δύσκολη και αναποτελεσματική.
Επιπλέον, όταν λύνετε τριγωνομετρικές εξισώσεις, δεν πρέπει ποτέ να ξεχνάτε ότι υπάρχουν πολλές πιθανές μέθοδοι επίλυσης.
Παράδειγμα 1. Βρείτε τον αριθμό των ριζών της εξίσωσης cos x = -1/2 στο διάστημα.
Διάλυμα:
Μέθοδος ΙΑς σχεδιάσουμε τις συναρτήσεις y = cos x και y = -1/2 και ας βρούμε τον αριθμό των κοινών σημείων τους στο διάστημα (Εικ. 1).
Δεδομένου ότι τα γραφήματα συναρτήσεων έχουν δύο κοινά σημείαστο διάστημα , τότε η εξίσωση περιέχει δύο ρίζες σε αυτό το διάστημα.
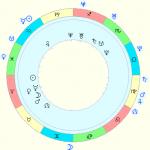
Μέθοδος II.Χρησιμοποιώντας έναν τριγωνομετρικό κύκλο (Εικ. 2), βρίσκουμε τον αριθμό των σημείων που ανήκουν στο διάστημα στο οποίο cos x = -1/2. Το σχήμα δείχνει ότι η εξίσωση έχει δύο ρίζες. 
μέθοδος III.Χρησιμοποιώντας τον τύπο για τις ρίζες της τριγωνομετρικής εξίσωσης, λύνουμε την εξίσωση cos x = -1/2.
x = ± τόξο (-1/2) + 2πk, k – ακέραιος (k € Z);
x = ± (π – arccos 1/2) + 2πk, k – ακέραιος (k € Z);
x = ± (π – π/3) + 2πk, k – ακέραιος (k € Z);
x = ± 2π/3 + 2πk, k – ακέραιος (k € Z).
Το διάστημα περιέχει τις ρίζες 2π/3 και -2π/3 + 2π, το k είναι ακέραιος. Έτσι, η εξίσωση έχει δύο ρίζες σε ένα δεδομένο διάστημα.
Απάντηση: 2.
Στο μέλλον, οι τριγωνομετρικές εξισώσεις θα επιλύονται χρησιμοποιώντας μία από τις προτεινόμενες μεθόδους, η οποία σε πολλές περιπτώσεις δεν αποκλείει τη χρήση άλλων μεθόδων.
Παράδειγμα 2. Βρείτε τον αριθμό των λύσεων της εξίσωσης tg (x + π/4) = 1 στο διάστημα [-2π; 2π].
Διάλυμα:
Χρησιμοποιώντας τον τύπο για τις ρίζες μιας τριγωνομετρικής εξίσωσης, παίρνουμε:
x + π/4 = arctan 1 + πk, k – ακέραιος (k € Z);
x + π/4 = π/4 + πk, k – ακέραιος (k € Z);
x = πk, k – ακέραιος (k € Z);
Το διάστημα [-2π; 2π] ανήκουν στους αριθμούς -2π; -π; 0; π; 2π. Άρα, η εξίσωση έχει πέντε ρίζες σε ένα δεδομένο διάστημα.
Απάντηση: 5.
Παράδειγμα 3. Βρείτε τον αριθμό των ριζών της εξίσωσης cos 2 x + sin x · cos x = 1 στο διάστημα [-π; π].
Διάλυμα:
Εφόσον 1 = sin 2 x + cos 2 x (η βασική τριγωνομετρική ταυτότητα), η αρχική εξίσωση παίρνει τη μορφή:
cos 2 x + sin x · cos x = sin 2 x + cos 2 x;
sin 2 x – sin x cos x = 0;
sin x(sin x – cos x) = 0. Το γινόμενο είναι ίσο με μηδέν, που σημαίνει ότι τουλάχιστον ένας από τους παράγοντες πρέπει να είναι ίσος με μηδέν, επομένως:
sin x = 0 ή sin x – cos x = 0.
Δεδομένου ότι οι τιμές της μεταβλητής στην οποία cos x = 0 δεν είναι οι ρίζες της δεύτερης εξίσωσης (το ημίτονο και το συνημίτονο του ίδιου αριθμού δεν μπορούν να είναι ίσα με μηδέν ταυτόχρονα), διαιρούμε και τις δύο πλευρές της δεύτερης εξίσωσης από cos x:
sin x = 0 ή sin x / cos x - 1 = 0.
Στη δεύτερη εξίσωση χρησιμοποιούμε το γεγονός ότι tg x = sin x / cos x, τότε:
sin x = 0 ή tan x = 1. Χρησιμοποιώντας τύπους έχουμε:
x = πk ή x = π/4 + πk, k – ακέραιος (k € Z).
Από την πρώτη σειρά ριζών μέχρι το διάστημα [-π; π] ανήκουν στους αριθμούς -π; 0; π. Από τη δεύτερη σειρά: (π/4 – π) και π/4.
Έτσι, οι πέντε ρίζες της αρχικής εξίσωσης ανήκουν στο διάστημα [-π; π].
Απάντηση: 5.
Παράδειγμα 4. Να βρείτε το άθροισμα των ριζών της εξίσωσης tg 2 x + сtg 2 x + 3tg x + 3сtgx + 4 = 0 στο διάστημα [-π; 1,1π].
Διάλυμα:
Ας ξαναγράψουμε την εξίσωση ως εξής:
tg 2 x + сtg 2 x + 3(tg x + сtgx) + 4 = 0 και κάντε μια αντικατάσταση.
Έστω tg x + сtgx = a. Ας τετραγωνίσουμε και τις δύο πλευρές της εξίσωσης:
(tg x + сtg x) 2 = a 2. Ας επεκτείνουμε τις αγκύλες:
tg 2 x + 2tg x · сtgx + сtg 2 x = a 2.
Αφού tg x · σtgx = 1, τότε tg 2 x + 2 + σtg 2 x = a 2, που σημαίνει
tg 2 x + сtg 2 x = a 2 – 2.
Τώρα η αρχική εξίσωση μοιάζει με:
a 2 – 2 + 3a + 4 = 0;
a 2 + 3a + 2 = 0. Χρησιμοποιώντας το θεώρημα του Vieta, βρίσκουμε ότι a = -1 ή a = -2.
Ας κάνουμε την αντίστροφη αντικατάσταση, έχουμε:
tg x + сtgx = -1 ή tg x + сtgx = -2. Ας λύσουμε τις εξισώσεις που προκύπτουν.
tg x + 1/tgx = -1 ή tg x + 1/tgx = -2.
Με την ιδιότητα δύο αμοιβαία αντίστροφων αριθμών προσδιορίζουμε ότι η πρώτη εξίσωση δεν έχει ρίζες και από τη δεύτερη εξίσωση έχουμε:
tg x = -1, δηλ. x = -π/4 + πk, k – ακέραιος (k € Z).
Το διάστημα [-π; 1,1π] ανήκουν στις ρίζες: -π/4; -π/4 + π. Το άθροισμά τους:
-π/4 + (-π/4 + π) = -π/2 + π = π/2.
Απάντηση: π/2.
Παράδειγμα 5. Βρείτε τον αριθμητικό μέσο όρο των ριζών της εξίσωσης sin 3x + sin x = sin 2x στο διάστημα [-π; 0,5π].
Διάλυμα:
Ας χρησιμοποιήσουμε τον τύπο sin α + sin β = 2sin ((α + β)/2) cos ((α – β)/2), τότε
sin 3x + sin x = 2sin ((3x + x)/2) cos ((3x – x)/2) = 2sin 2x cos x και η εξίσωση γίνεται
2sin 2x cos x = αμαρτία 2x;
2sin 2x · cos x – sin 2x = 0. Ας πάρουμε τον κοινό παράγοντα sin 2x από αγκύλες
sin 2x(2cos x – 1) = 0. Λύστε την εξίσωση που προκύπτει:
sin 2x = 0 ή 2cos x – 1 = 0; 
sin 2x = 0 ή cos x = 1/2;
2x = πk ή x = ±π/3 + 2πk, k – ακέραιος (k € Z).
Έτσι έχουμε ρίζες
x = πk/2, x = π/3 + 2πk, x = -π/3 + 2πk, k – ακέραιος (k € Z).
Το διάστημα [-π; 0,5π] ανήκουν στις ρίζες -π; -π/2; 0; π/2 (από την πρώτη σειρά ριζών). π/3 (από τη δεύτερη σειρά). -π/3 (από την τρίτη σειρά). Ο αριθμητικός τους μέσος όρος είναι:
(-π – π/2 + 0 + π/2 + π/3 – π/3)/6 = -π/6.
Απάντηση: -π/6.
Παράδειγμα 6. Βρείτε τον αριθμό των ριζών της εξίσωσης sin x + cos x = 0 στο διάστημα [-1,25π; 2π].
Διάλυμα:
Αυτή η εξίσωση είναι μια ομοιογενής εξίσωση πρώτου βαθμού. Ας διαιρέσουμε και τα δύο μέρη του με cosx (οι τιμές της μεταβλητής στην οποία cos x = 0 δεν είναι οι ρίζες αυτής της εξίσωσης, αφού το ημίτονο και το συνημίτονο του ίδιου αριθμού δεν μπορούν να είναι ίσα με μηδέν ταυτόχρονα). Η αρχική εξίσωση είναι:
x = -π/4 + πk, k – ακέραιος (k € Z).
Το διάστημα [-1,25π; 2π] ανήκουν στις ρίζες -π/4; (-π/4 + π); και (-π/4 + 2π).
Έτσι, το δεδομένο διάστημα περιέχει τρεις ρίζες της εξίσωσης.
Απάντηση: 3.
Μάθετε να κάνετε το πιο σημαντικό πράγμα - φανταστείτε ξεκάθαρα ένα σχέδιο για την επίλυση ενός προβλήματος και τότε οποιαδήποτε τριγωνομετρική εξίσωση θα είναι στη διάθεσή σας.
Έχετε ακόμα ερωτήσεις; Δεν ξέρετε πώς να λύσετε τριγωνομετρικές εξισώσεις;
Για να λάβετε βοήθεια από έναν δάσκαλο, εγγραφείτε.
ιστοσελίδα, κατά την πλήρη ή μερική αντιγραφή υλικού, απαιτείται σύνδεσμος προς την πηγή.
Στόχος του μαθήματος:
- Επαναλάβετε τους τύπους για την επίλυση των απλούστερων τριγωνομετρικών εξισώσεων.
- Εξετάστε τρεις κύριες μεθόδους επιλογής ριζών κατά την επίλυση τριγωνομετρικών εξισώσεων:
επιλογή με ανισότητα, επιλογή με παρονομαστή και επιλογή ανά διάστημα.
Εξοπλισμός:Εξοπλισμός πολυμέσων.
Μεθοδικό σχόλιο.
- Εφιστήστε την προσοχή των μαθητών στη σημασία του θέματος του μαθήματος.
- Οι τριγωνομετρικές εξισώσεις στις οποίες είναι απαραίτητο να επιλέξετε ρίζες βρίσκονται συχνά σε θεματικές δοκιμές της Ενιαίας Κρατικής Εξέτασης.
Η επίλυση τέτοιων προβλημάτων επιτρέπει στους μαθητές να εδραιώσουν και να εμβαθύνουν τις γνώσεις που είχαν αποκτήσει προηγουμένως.
Πρόοδος μαθήματος
Επανάληψη. Είναι χρήσιμο να υπενθυμίσουμε τους τύπους για την επίλυση των απλούστερων τριγωνομετρικών εξισώσεων (οθόνη).
| Αξίες | Εξίσωση | Τύποι επίλυσης εξισώσεων |
| sinx=α | ||
| sinx=α | στο η εξίσωση δεν έχει λύσεις | |
| a=0 | sinx=0 | |
| a=1 | sinx= 1 |
|
| a= -1 | sinx= -1 |
|
| cosx=a | ||
| cosx=a | η εξίσωση δεν έχει λύσεις | |
| a=0 | cosx=0 |
|
| a=1 | cosx= 1 | |
| a= -1 | cosx= -1 |
|
| tgx=a | ||
| ctgx=a |
Όταν επιλέγετε root in τριγωνομετρικές εξισώσειςγράφοντας λύσεις σε εξισώσεις sinx=a, сosx=aστο σύνολό της είναι πιο δικαιολογημένη. Αυτό θα το φροντίσουμε όταν λύνουμε προβλήματα.
Επίλυση εξισώσεων.
Εργο. Λύστε την εξίσωση ![]()
Διάλυμα.Αυτή η εξίσωση είναι ισοδύναμη με το ακόλουθο σύστημα


Σκεφτείτε έναν κύκλο. Ας σημειώσουμε τις ρίζες κάθε συστήματος πάνω του και ας σημειώσουμε με τόξο εκείνο το τμήμα του κύκλου όπου η ανισότητα ( ρύζι. 1)

Ρύζι. 1
Το καταλαβαίνουμε ![]() δεν μπορεί να είναι λύση στην αρχική εξίσωση.
δεν μπορεί να είναι λύση στην αρχική εξίσωση.
Απάντηση:
![]()
Σε αυτό το πρόβλημα επιλέξαμε ρίζες με ανισότητα.
Στο επόμενο πρόβλημα θα πραγματοποιήσουμε επιλογή με τον παρονομαστή. Για να γίνει αυτό, θα επιλέξουμε τις ρίζες του αριθμητή, αλλά έτσι ώστε να μην είναι οι ρίζες του παρονομαστή.
Εργασία 2.Λύστε την εξίσωση.
![]()
Διάλυμα. Ας γράψουμε τη λύση της εξίσωσης χρησιμοποιώντας διαδοχικές ισοδύναμες μεταβάσεις.

Όταν λύνουμε την εξίσωση και την ανισότητα του συστήματος, στη λύση βάζουμε διαφορετικά γράμματα, που αντιπροσωπεύουν ακέραιους αριθμούς. Εικονίζοντας στο σχήμα, σημειώνουμε στον κύκλο τις ρίζες της εξίσωσης με κύκλους και τις ρίζες του παρονομαστή με σταυρούς (Εικ. 2.)


Ρύζι. 2
Από το σχήμα φαίνεται ξεκάθαρα ότι ![]() – λύση της αρχικής εξίσωσης.
– λύση της αρχικής εξίσωσης.
Ας επιστήσουμε την προσοχή των μαθητών στο γεγονός ότι ήταν ευκολότερο να επιλέξουν ρίζες χρησιμοποιώντας ένα σύστημα με γραφική παράσταση των αντίστοιχων σημείων στον κύκλο.
Απάντηση:
![]()
Εργασία 3.Λύστε την εξίσωση
3sin2x = 10 cos 2 x – 2/
Βρείτε όλες τις ρίζες της εξίσωσης που ανήκουν στο τμήμα.
Διάλυμα.Σε αυτό το πρόβλημα, οι ρίζες επιλέγονται στο διάστημα, το οποίο καθορίζεται από την κατάσταση του προβλήματος. Η επιλογή ριζών σε ένα διάστημα μπορεί να γίνει με δύο τρόπους: με αναζήτηση στις τιμές μιας μεταβλητής για ακέραιους αριθμούς ή με επίλυση μιας ανισότητας.
Σε αυτή την εξίσωση, θα επιλέξουμε τις ρίζες χρησιμοποιώντας την πρώτη μέθοδο και στο επόμενο πρόβλημα, λύνοντας την ανισότητα.
Ας χρησιμοποιήσουμε το κύριο τριγωνομετρική ταυτότητακαι ο τύπος διπλής γωνίας για το ημίτονο. Παίρνουμε την εξίσωση
6sinxcosx = 10cos 2 x – sin 2 x – cos 2 x,εκείνοι. sin 2 x – 9cos 2 x+ 6sinxcosx = 0
Επειδή αλλιώς sinx = 0, το οποίο δεν μπορεί να είναι, αφού δεν υπάρχουν γωνίες για τις οποίες το ημίτονο και το συνημίτονο είναι και τα δύο ίσα με μηδέν, που σημαίνει αμαρτία 2 x+ cos 2 x = 0.
Ας διαιρέσουμε και τις δύο πλευρές της εξίσωσης με cos 2 x.παίρνουμε tg 2 x+ 6tgx – 9 = 0/
Αφήνω tgx = t, Τότε t 2 + 6t – 9 = 0, t 1 = 2, t 2 = –8.
tgx = 2 ή tg = –8;
Ας εξετάσουμε κάθε σειρά ξεχωριστά, βρίσκοντας σημεία μέσα στο διάστημα, και ένα σημείο αριστερά και δεξιά από αυτό.
Αν k=0, Αυτό x=arctg2. Αυτή η ρίζα ανήκει στο υπό εξέταση διάστημα.
Αν k=1, Αυτό x=arctg2+.Στο υπό εξέταση διάστημα ανήκει και αυτή η ρίζα.
Αν k=2, Αυτό ![]() . Είναι ξεκάθαρο ότι δεδομένη ρίζαδεν ανήκει στο κενό μας.
. Είναι ξεκάθαρο ότι δεδομένη ρίζαδεν ανήκει στο κενό μας.
Θεωρήσαμε ένα σημείο στα δεξιά αυτού του διαστήματος, έτσι k=3,4,…δεν λαμβάνονται υπόψη.
Αν k = –1,παίρνουμε – δεν ανήκει στο διάστημα .
Αξίες k = –2, –3,…δεν λαμβάνονται υπόψη.
Έτσι, από αυτή τη σειρά δύο ρίζες ανήκουν στο διάστημα
Παρόμοια με την προηγούμενη περίπτωση, φροντίζουμε όταν n = 0Και n = 2,και, επομένως, πότε p = –1, –2,…p = 3,4,…θα πάρουμε ρίζες που δεν ανήκουν στο διάστημα. Μόνο όταν n=1λαμβάνουμε , που ανήκουν σε αυτό το διάστημα.
Απάντηση:
Εργασία 4.Λύστε την εξίσωση 6sin 2 x+2sin 2 2x=5και να δηλώσετε τις ρίζες που ανήκουν στο διάστημα .
Διάλυμα.Ας δώσουμε την εξίσωση 6sin 2 x+2sin 2 2x=5Να τετραγωνική εξίσωσησχετικά cos2x.
Οπου cos2x ![]()
Εδώ εφαρμόζουμε τη μέθοδο επιλογής στο διάστημα χρησιμοποιώντας διπλή ανισότητα
![]()
Επειδή Ναπαίρνει μόνο ακέραιες τιμές, είναι μόνο δυνατό k=2,k=3.
Στο k=2παίρνουμε , με k=3θα λάβουμε.
Απάντηση: ![]()
Μεθοδολογικός σχολιασμός.Συνιστάται ο δάσκαλος να λύσει αυτά τα τέσσερα προβλήματα στον πίνακα με τη συμμετοχή των μαθητών. Για να λύσετε το επόμενο πρόβλημα, είναι καλύτερα να καλέσετε έναν δυνατό μαθητή στην κόρη σας, δίνοντάς του τη μέγιστη ανεξαρτησία στη λογική.
Εργασία 5.Λύστε την εξίσωση

Διάλυμα.Μετασχηματίζοντας τον αριθμητή, ανάγουμε την εξίσωση σε απλούστερη μορφή

Η εξίσωση που προκύπτει είναι ισοδύναμη με το συνδυασμό δύο συστημάτων:

Επιλογή ριζών στο διάστημα (0; 5) Ας το κάνουμε με δύο τρόπους. Η πρώτη μέθοδος είναι για το πρώτο σύστημα του αδρανούς, η δεύτερη μέθοδος είναι για το δεύτερο σύστημα του αδρανούς.
, 0
Επειδή Ναείναι ακέραιος λοιπόν k=1. Τότε x =– λύση της αρχικής εξίσωσης.
Εξετάστε το δεύτερο σύστημα του αθροίσματος

Αν n=0, Αυτό ![]() . Στο n = -1; -2;…δεν θα υπάρξουν λύσεις.
. Στο n = -1; -2;…δεν θα υπάρξουν λύσεις.
Αν n=1, ![]() – λύση του συστήματος και, επομένως, της αρχικής εξίσωσης.
– λύση του συστήματος και, επομένως, της αρχικής εξίσωσης.
Αν n=2, Αυτό
Δεν θα υπάρξουν αποφάσεις.