Trigonometrik fonksiyonlar içeren eşitsizlikler çözülürken bunlar cos(t)>a, sint(t)=a ve benzeri formdaki en basit eşitsizliklere indirgenir. Ve zaten en basit eşitsizlikler çözüldü. Hadi bakalım çeşitli örnekler Basit trigonometrik eşitsizlikleri çözmenin yolları.
Örnek 1. Sin(t) > = -1/2 eşitsizliğini çözün.
Bir birim çember çizin. Sin(t) tanımı gereği y koordinatı olduğundan, Oy ekseninde y = -1/2 noktasını işaretliyoruz. Üzerinden Ox eksenine paralel düz bir çizgi çiziyoruz. Düz çizginin birim çember grafiğiyle kesiştiği noktada Pt1 ve Pt2 noktalarını işaretleyin. Koordinatların kökenini Pt1 ve Pt2 noktalarına iki parça ile bağlarız.
Bu eşitsizliğin çözümü birim çemberin bu noktaların üzerinde yer alan tüm noktaları olacaktır. Başka bir deyişle çözüm l yayı olacaktır. Şimdi keyfi bir noktanın l yayına ait olacağı koşulları belirtmek gerekir.
Pt1 sağ yarım dairede yer alır, ordinatı -1/2'dir, bu durumda t1=arcsin(-1/2) = - pi/6 olur. Pt1 noktasını tanımlamak için aşağıdaki formülü yazabilirsiniz:
t2 = pi - arcsin(-1/2) = 7*pi/6. Sonuç olarak t için aşağıdaki eşitsizliği elde ederiz:
Eşitsizlikleri koruyoruz. Sinüs fonksiyonu periyodik olduğundan çözümlerin her 2*pi'de bir tekrarlanacağı anlamına gelir. Bu koşulu t için elde edilen eşitsizliğe ekliyoruz ve cevabı yazıyoruz.
Cevap: -pi/6+2*pi*n< = t < = 7*pi/6 + 2*pi*n, при любом целом n.
Örnek 2. Cos(t) eşitsizliğini çözme<1/2.
Birim çember çizelim. Tanıma göre cos(t) x koordinatı olduğundan Ox eksenindeki grafikte x = 1/2 noktasını işaretliyoruz.
Bu noktadan Oy eksenine paralel düz bir çizgi çiziyoruz. Düz çizginin birim çember grafiğiyle kesiştiği noktada Pt1 ve Pt2 noktalarını işaretleyin. Koordinatların kökenini Pt1 ve Pt2 noktalarına iki parça ile bağlarız.

Çözümler birim çemberin l yayına ait tüm noktaları olacaktır. t1 ve t2 noktalarını bulalım.
t1 = arccos(1/2) = pi/3.
t2 = 2*pi - arccos(1/2) = 2*pi-pi/3 = 5*pi/6.
t için eşitsizliği elde ettik: pi/3 Kosinüs periyodik bir fonksiyon olduğundan çözümler her 2*pi'de bir tekrarlanacaktır. Bu koşulu t için elde edilen eşitsizliğe ekliyoruz ve cevabı yazıyoruz. Cevap: pi/3+2*pi*n Örnek 3. tg(t) eşitsizliğini çözün< = 1. Teğet periyodu pi'ye eşittir. Sağ yarım dairenin (-pi/2;pi/2) aralığına ait çözümler bulalım. Daha sonra teğetin periyodikliğini kullanarak bu eşitsizliğin tüm çözümlerini yazıyoruz. Bir birim çember çizelim ve üzerine teğetlerden oluşan bir çizgi çizelim. Eğer t eşitsizliğin bir çözümü ise, o zaman T = tg(t) noktasının ordinatı 1'den küçük veya 1'e eşit olmalıdır. Bu tür noktaların kümesi AT ışınını oluşturacaktır. Bu ışının noktalarına karşılık gelecek Pt noktaları kümesi l yayındır. Üstelik P(-pi/2) noktası bu yaya ait değil. Eşitsizlikler a › b biçimindeki ilişkilerdir; burada a ve b, en az bir değişken içeren ifadelerdir. Eşitsizlikler katı - ‹, › olabilir ve katı olmayan - ≥, ≤ olabilir. Trigonometrik eşitsizlikler şu formdaki ifadelerdir: F(x) › a, F(x) ‹ a, F(x) ≤ a, F(x) ≥ a, burada F(x) bir veya daha fazla trigonometrik fonksiyonla temsil edilir . En basit trigonometrik eşitsizliğe bir örnek: sin x ‹ 1/2. Bu tür problemleri grafiksel olarak çözmek gelenekseldir; bunun için iki yöntem geliştirilmiştir. Sin x ‹ 1/2 eşitsizliği koşullarını karşılayan bir aralık bulmak için aşağıdaki adımları uygulamanız gerekir: Bir ifadede katı işaretler mevcut olduğunda kesişim noktaları çözüm değildir. Bir sinüzoidin en küçük pozitif periyodu 2π olduğundan cevabı şu şekilde yazıyoruz: İfadenin işaretleri kesin değilse, çözüm aralığı köşeli parantez - içine alınmalıdır. Sorunun cevabı aşağıdaki eşitsizlik olarak da yazılabilir: Benzer problemler trigonometrik çember kullanılarak kolayca çözülebilir. Cevap bulma algoritması çok basittir: Sin x › 1/2 eşitsizliği örneğini kullanarak çözümün aşamalarını analiz edelim. Daire üzerinde α ve β noktaları işaretlenmiştir - değerler Yayın α ve β'nın üzerinde bulunan noktaları, verilen eşitsizliği çözme aralığıdır. Cos için bir örnek çözmeniz gerekiyorsa, cevap yayı OY'ye değil OX eksenine simetrik olarak yerleştirilecektir. Sin ve cos için çözüm aralıkları arasındaki farkı metinde aşağıdaki diyagramlarda düşünebilirsiniz. Teğet ve kotanjant eşitsizliklerin grafik çözümleri hem sinüs hem de kosinüs çözümlerinden farklı olacaktır. Bu, fonksiyonların özelliklerinden kaynaklanmaktadır. Arktanjant ve arkkotanjant trigonometrik daireye teğettir ve her iki fonksiyon için minimum pozitif periyot π'dir. İkinci yöntemi hızlı ve doğru bir şekilde kullanmak için sin, cos, tg ve ctg değerlerinin hangi eksende çizildiğini hatırlamanız gerekir. Teğet teğet OY eksenine paralel uzanır. Arctan a'nın değerini birim çember üzerine çizersek, gerekli ikinci nokta köşegen çeyrekte yer alacaktır. Açılar Bunlar fonksiyon için kırılma noktalarıdır, çünkü grafik onlara yönelir ancak asla onlara ulaşmaz. Kotanjant durumunda, teğet OX eksenine paralel uzanır ve fonksiyon π ve 2π noktalarında kesintiye uğrar. Eşitsizlik fonksiyonunun argümanı yalnızca bir değişkenle değil, bilinmeyeni içeren bir ifadenin tamamıyla temsil ediliyorsa, o zaman karmaşık bir eşitsizlikten bahsediyoruz demektir. Bunu çözme süreci ve prosedürü yukarıda açıklanan yöntemlerden biraz farklıdır. Aşağıdaki eşitsizliğe bir çözüm bulmamız gerektiğini varsayalım: Grafiksel çözüm, keyfi olarak seçilen x değerlerini kullanarak sıradan bir sinüzoid y = sin x oluşturmayı içerir. Grafiğin kontrol noktalarının koordinatlarını içeren bir tablo hesaplayalım: Sonuç güzel bir eğri olmalıdır. Çözüm bulmayı kolaylaştırmak için karmaşık fonksiyon argümanını değiştirelim Çoğu öğrenci trigonometrik eşitsizliklerden hoşlanmaz. Ama boşuna. Bir karakterin söylediği gibi, “Onları nasıl pişireceğini bilmiyorsun” Peki nasıl "pişirilir" ve sinüs ile eşitsizliğin neyle sunulacağını bu makalede çözeceğiz. Bunu en basit şekilde birim çemberi kullanarak çözeceğiz. Yani öncelikle aşağıdaki algoritmaya ihtiyacımız var. Önemli: d verilen algoritma çalışmıyor$\sin(x) > 1 formundaki eşitsizlikler için; \ \sin(x) \geq 1, \ \sin(x)< -1, \ \sin{x} \leq -1$. В строгом случае эти неравенства не имеют решений, а в нестрогом – решение сводится к решению уравнения $\sin{x} = 1$ или $\sin{x} = -1$. Yukarıdaki algoritmayı kullanmadan mantıksal olarak çözülmesi çok daha uygun olan aşağıdaki durumları da not etmek önemlidir. Özel durum 1. Eşitsizliği çözün: $\sin(x)\leq 1.$ $y=\sin(x)$ trigonometrik fonksiyonunun değer aralığının $1$ modülünden büyük olmaması nedeniyle eşitsizliğin sol tarafı herhangi bir zamanda Tanım alanından $x$ (ve sinüs tanım kümesinin tamamı gerçek sayılardır) $1$'dan fazla değildir. Ve bu nedenle yanıtta şunu yazıyoruz: $x \in R$. Sonuçlar: $\sin(x)\geq -1.$ Özel durum 2. Eşitsizliği çözün: $\sin(x)< 1.$ Özel durum 1'e benzer bir akıl yürütme uygulayarak, $\sin(x) = 1$ denkleminin çözümü olan noktalar hariç, tüm $x \in R$ için eşitsizliğin sol tarafının $1$'dan küçük olduğunu bulduk. Bu denklemi çözersek: $x = (-1)^(n)\arcsin(1)+ \pi n = (-1)^(n)\frac(\pi)(2) + \pi n.$ Ve bu nedenle yanıtta şunu yazıyoruz: $x \in R \backslash \left\((-1)^(n)\frac(\pi)(2) + \pi n\right\)$. Sonuçlar: eşitsizlik benzer şekilde çözülür $\sin(x) > -1.$ Örnek 1: Eşitsizliği çözün: $\sin(x) \geq \frac(1)(2).$ Böylece çözüm şu şekli alacaktır: $x \in \left[\frac(\pi)(6) + 2\pi n; \frac(5\pi)(6) + 2 \pi n\right], \n \in Z.$ Örnek 2: Eşitsizliği çözün: $\sin(x)< -\frac{1}{2}$ Sinüs ekseninde $-\frac(1)(2)$ koordinatını işaretleyip kosinüs eksenine paralel ve bu noktadan geçen düz bir çizgi çizelim. Kesişme noktalarını işaretleyelim. Eşitsizlik katı olduğundan gölgelenmeyecekler. Eşitsizlik işareti $<$, а, значит, закрашиваем область ниже прямой, т.е. меньший полукруг. Неравенство превращаем в равенство и решаем его: $\sin(x)=-\frac(1)(2)$ $x=(-1)^(n)\arcsin(\left(-\frac(1)(2)\right))+ \pi n =(-1)^(n+1)\frac(\pi )(6) + \pi n$. Ayrıca $n=0$ varsayarsak, ilk kesişim noktasını buluruz: $x_(1)=-\frac(\pi)(6)$. Alanımız ilk noktadan itibaren negatif yönde gidiyor, yani $n$'ı $-1$'a eşit olarak ayarladık: $x_(2)=(-1)^(-1+1)\frac(\pi)( 6) + \pi \cdot (-1) = -\pi + \frac(\pi)(6) = -\frac(5\pi)(6)$. $x \in \left(-\frac(5\pi)(6) + 2\pi n; -\frac(\pi)(6) + 2 \pi n\right), \n \in Z.$ Örnek 3: Eşitsizliği çözün: $1 – 2\sin(\left(\frac(x)(4)+\frac(\pi)(6)\right)) \leq 0.$ Bu örnek bir algoritma kullanılarak hemen çözülemez. İlk önce onu dönüştürmeniz gerekiyor. Bir denklemle yapacağımız şeyin aynısını yaparız, ancak işareti unutmayız. Negatif bir sayıya bölmek veya çarpmak onu tersine çevirir! O halde trigonometrik fonksiyon içermeyen her şeyi sağ tarafa taşıyalım. Şunu elde ederiz: $- 2\sin(\left(\frac(x)(4)+\frac(\pi)(6)\right)) \leq -1.$ Sol ve sağ tarafları $-2$'a bölelim (işaretini unutmayın!). Sahip olacağız: $\sin(\left(\frac(x)(4)+\frac(\pi)(6)\right)) \geq \frac(1)(2).$ Yine algoritma kullanarak çözemeyeceğimiz bir eşitsizlikle karşı karşıyayız. Ancak burada değişkeni değiştirmek yeterlidir: $t=\frac(x)(4)+\frac(\pi)(6).$ Algoritma kullanılarak çözülebilecek bir trigonometrik eşitsizlik elde ediyoruz: $\sin(t) \geq \frac(1)(2).$ Bu eşitsizlik Örnek 1'de çözülmüştür, dolayısıyla cevabı buradan ödünç alalım: $t \in \left[\frac(\pi)(6) + 2\pi n; \frac(5\pi)(6) + 2 \pi n\sağ].$ Ancak karar henüz bitmedi. Orijinal değişkene geri dönmemiz gerekiyor. $(\frac(x)(4)+\frac(\pi)(6)) \in \left[\frac(\pi)(6) + 2\pi n; \frac(5\pi)(6) + 2 \pi n\sağ].$ Aralığı bir sistem olarak düşünelim: $\left\(\begin(array)(c) \frac(x)(4)+\frac(\pi)(6) \geq \frac(\pi)(6) + 2\pi n, \\ \frac(x)(4)+\frac(\pi)(6) \leq \frac(5\pi)(6) + 2 \pi n. Sistemin sol tarafında aralığa ait ($\frac(x)(4)+\frac(\pi)(6)$) ifadesi bulunmaktadır. Aralığın sol sınırı ilk eşitsizlikten, sağ sınırı ise ikinci eşitsizlikten sorumludur. Dahası, parantezler önemli bir rol oynar: eğer parantez kare ise, o zaman eşitsizlik gevşetilecektir ve eğer yuvarlaksa, o zaman katı olacaktır. görevimiz soldan $x$ almak her iki eşitsizlikte. $\frac(\pi)(6)$'ı sol taraftan sağ tarafa taşıyalım, şunu elde ederiz: $\left\(\begin(array)(c) \frac(x)(4) \geq \frac(\pi)(6) + 2\pi n -\frac(\pi)(6), \\ \frac(x)(4) \leq \frac(5\pi)(6) + 2 \pi n – \frac(\pi)(6) \end(array) \right.$. Basitleştirerek şunları elde edeceğiz: $\left\(\begin(array)(c) \frac(x)(4) \geq 2\pi n, \\ \frac(x)(4) \leq \frac(2\pi)(3) + 2 \pi n \end(array) \right.$ Sol ve sağ tarafları $4$ ile çarparsak şunu elde ederiz: $\left\(\begin(array)(c) x \geq 8\pi n, \\ x \leq \frac(8\pi)(3) + 8 \pi n.\end(array) \right. $ Sistemi aralığa monte ederek cevabı elde ederiz: $x \in \left[ 8\pi n; \frac(8\pi)(3) + 8 \pi n\right], \n \in Z.$ TRİGONOMETRİK EŞİTSİZLİKLERİ ÇÖZME YÖNTEMLERİ
Alaka düzeyi.
Tarihsel olarak trigonometrik denklemlere ve eşitsizliklere okul müfredatında özel bir yer verilmiştir. Trigonometrinin okul dersinin ve genel olarak tüm matematik biliminin en önemli bölümlerinden biri olduğunu söyleyebiliriz. Trigonometrik denklemler ve eşitsizlikler, hem içerik hem de ortaokul matematik dersinde merkezi yerlerden birini işgal eder. eğitim materyali ve çalışmaları sırasında oluşturulabilecek ve oluşturulması gereken ve teorik ve uygulamalı nitelikteki çok sayıda problemin çözümünde uygulanan eğitimsel ve bilişsel faaliyet yöntemlerine göre. Trigonometrik denklemleri ve eşitsizlikleri çözmek, öğrencilerin trigonometrideki tüm eğitim materyalleriyle ilgili bilgilerini (örneğin, trigonometrik fonksiyonların özellikleri, trigonometrik ifadeleri dönüştürme yöntemleri vb.) sistematik hale getirmek için ön koşulları oluşturur ve çalışılan materyalle etkili bağlantılar kurmayı mümkün kılar. cebirde (denklemler, denklemlerin denkliği, eşitsizlikler, cebirsel ifadelerin özdeş dönüşümleri vb.). Başka bir deyişle, trigonometrik denklemleri ve eşitsizlikleri çözmeye yönelik tekniklerin değerlendirilmesi, bu becerilerin bir nevi yeni içeriğe aktarılmasını içerir. Teorinin önemi ve sayısız uygulaması, seçilen konunun uygunluğunun kanıtıdır. Bu da ders çalışmasının amaçlarını, hedeflerini ve araştırma konusunu belirlemenize olanak tanır. Çalışmanın amacı:
Mevcut trigonometrik eşitsizlik türlerini, bunları çözmek için temel ve özel yöntemleri genelleştirmek, okul çocukları tarafından trigonometrik eşitsizlikleri çözmek için bir dizi problem seçmek. Araştırma hedefleri:
1. Araştırma konusuyla ilgili mevcut literatürün analizine dayanarak materyali sistemleştirin. 2. “Trigonometrik eşitsizlikler” konusunu pekiştirmek için gerekli bir dizi görevi sağlayın. Çalışmanın amacı
okul matematik dersinde trigonometrik eşitsizliklerdir. Araştırma konusu:
Trigonometrik eşitsizlik türleri ve bunları çözme yöntemleri. Teorik önemi
materyali sistematize etmektir. Pratik önemi:
teorik bilginin problem çözümünde uygulanması; trigonometrik eşitsizlikleri çözmek için ana ortak yöntemlerin analizi. Araştırma yöntemleri
: bilimsel literatürün analizi, edinilen bilgilerin sentezi ve genelleştirilmesi, problem çözme analizi, eşitsizlikleri çözmek için en uygun yöntemlerin araştırılması. §1.
Trigonometrik eşitsizlik türleri ve bunları çözmenin temel yöntemleri
1.1. En basit trigonometrik eşitsizlikler
Veya > işaretiyle birbirine bağlanan iki trigonometrik ifadeye trigonometrik eşitsizlikler denir. Trigonometrik bir eşitsizliği çözmek, eşitsizliğin karşılandığı eşitsizliğin içerdiği bilinmeyenlerin değer kümesini bulmak anlamına gelir. Trigonometrik eşitsizliklerin ana kısmı, bunları en basit çözüme indirgeyerek çözülür: Bu bir çarpanlara ayırma yöntemi, değişken değişikliği olabilir ( En basit eşitsizlikler iki şekilde çözülebilir: birim çember kullanılarak veya grafiksel olarak. İzin vermekf(x
– temel trigonometrik fonksiyonlardan biri. Eşitsizliği çözmek için Eşitsizlikleri çözmek için bir algoritma örneği verelim Eşitsizliği çözmek için algoritma 1. Bir sayının sinüsünün tanımını formüle edinX
birim çember üzerinde. 3. Ordinat ekseninde koordinatın bulunduğu noktayı işaretleyinA
.
4. Bu noktadan OX eksenine paralel bir çizgi çizin ve daire ile kesişme noktalarını işaretleyin. 5. Tüm noktalarının koordinatı şundan küçük olan bir daire yayı seçin:A
.
6. Turun yönünü (saat yönünün tersine) belirtiniz ve aralığın sonuna fonksiyonun periyodunu ekleyerek cevabı yazınız.2πn
,
Eşitsizliği çözmek için algoritma 1. Bir sayının tanjantının tanımını formüle edinX
birim çember üzerinde. 2. Bir birim çember çizin. 3. Bir teğet çizgisi çizin ve üzerinde koordinat bulunan bir noktayı işaretleyinA
.
4. Bu noktayı orijine bağlayın ve ortaya çıkan parçanın birim çemberle kesişme noktasını işaretleyin. 5. Tüm noktalarının teğet doğru üzerinde koordinatları şu değerlerden küçük olan bir daire yayı seçin:A
.
6. Çapraz geçişin yönünü belirtin ve fonksiyonun tanım alanını dikkate alarak bir nokta ekleyerek cevabı yazınπn
,
En basit denklemlerin çözümlerinin grafiksel yorumu ve eşitsizlikleri genel biçimde çözmek için kullanılan formüller ekte (Ek 1 ve 2) belirtilmiştir. Örnek 1.
Eşitsizliği çöz Birim çembere düz bir çizgi çizin Tüm anlamlarsen
NM aralığında daha büyüktür
AMB yayının tüm noktaları bu eşitsizliği karşılar. Tüm dönüş açılarında büyük Şekil 1 Böylece eşitsizliğin çözümü aralıktaki tüm değerler olacaktır. onlar. Cevap: 1.2. Grafik yöntemi
Uygulamada trigonometrik eşitsizliklerin çözümü için grafiksel yöntemin sıklıkla yararlı olduğu ortaya çıkar. Eşitsizlik örneğini kullanarak yöntemin özünü ele alalım 1. Argüman karmaşıksa (öngörüden farklıysa)X
), ardından şununla değiştirin:T
.
2. Tek bir koordinat düzleminde inşa ediyoruzoyuncak
fonksiyon grafikleri 3. Böyle buluyoruzgrafiklerin iki bitişik kesişme noktası, bunların arasındasinüs dalgasıbulunandaha yüksek
doğrudan 4. Argüman için çifte eşitsizliği yazınT
kosinüs periyodu dikkate alınarak (T
Bulunan apsisler arasında olacaktır). 5. Ters bir değişiklik yapın (orijinal argümana dönün) ve değeri ifade edinX
Çifte eşitsizlikten cevabı sayısal aralık şeklinde yazıyoruz. Örnek 2.
Eşitsizliği çözün: . Eşitsizlikleri grafiksel yöntemle çözerken, fonksiyonların grafiklerini mümkün olduğunca doğru bir şekilde oluşturmak gerekir. Eşitsizliği forma dönüştürelim: Tek koordinat sisteminde fonksiyonların grafiklerini oluşturalım Şekil 2 Fonksiyonların grafikleri bir noktada kesişir.A
koordinatlarla Cevap: 1.3. Cebirsel yöntem
Çoğunlukla orijinal trigonometrik eşitsizlik, iyi seçilmiş bir ikame yoluyla cebirsel (rasyonel veya irrasyonel) eşitsizliğe indirgenebilir. Bu yöntem bir eşitsizliğin dönüştürülmesini, bir ikame getirilmesini veya bir değişkenin değiştirilmesini içerir. Bu yöntemin uygulanmasına ilişkin belirli örneklere bakalım. Örnek 3.
En basit forma indirgeme Şekil 3 Cevap: Örnek 4.
Eşitsizliği çözün: ODZ: Formülleri kullanma: Eşitsizliği şu şekilde yazalım: Ya da inanmak Son eşitsizliği aralık yöntemini kullanarak çözerek şunu elde ederiz: Şekil 4 Şekil 5 Cevap: 1.4. Aralık yöntemi
Aralık yöntemini kullanarak trigonometrik eşitsizlikleri çözmek için genel şema: Trigonometrik formülleri kullanarak çarpanlara ayırma. Fonksiyonun süreksizlik noktalarını ve sıfırlarını bulun ve bunları çemberin üzerine yerleştirin. Herhangi bir noktayı alİLE
(ancak daha önce bulunamadı) ve ürünün işaretini bulun. Çarpım pozitifse, açıya karşılık gelen ışının üzerine birim çemberin dışına bir nokta yerleştirin. Aksi takdirde noktayı dairenin içine yerleştirin. Bir nokta çift sayıda ortaya çıkıyorsa ona çift katlı nokta diyoruz; tek sayıda ortaya çıkıyorsa ona tek katlı nokta diyoruz. Yayları şu şekilde çizin: bir noktadan başlayınİLE
, eğer bir sonraki nokta tek katlıysa yay bu noktada daireyi keser, ancak nokta çift katlıysa kesişmez. Çemberin arkasındaki yaylar pozitif aralıklardır; dairenin içinde negatif boşluklar var. Örnek 5.
Eşitsizliği çözün İlk serinin noktaları: İkinci serinin noktaları: Her nokta tek sayıda ortaya çıkar, yani tüm noktalar tek katlıdır. Ürünün işaretini şuradan öğrenelim. Pirinç. 6 Cevap: Örnek 6
. Eşitsizliği çöz.
Çözüm:
İfadenin sıfırlarını bulalım .
AlmakaeM :
Birim çember serisi değerleri hakkındaX
1
noktalarla temsil edilir Şimdi sayıyı bırakalım Yani tam noktaA
açıyı oluşturan ışın üzerinde seçilmelidir Şimdi noktadanA
işaretli tüm noktalara sırayla dalgalı, sürekli bir çizgi çizin. Ve bazı noktalarda Şekil 7 Son cevap: Not.
Birim çember üzerinde işaretlenen tüm noktaları geçtikten sonra dalgalı bir çizgi noktaya geri döndürülemiyorsaA
,
Çemberin “yasadışı” bir yerden geçilmemesi, çözümde bir hata yapıldığı, yani tek sayıda kökün kaçırıldığı anlamına gelir. Cevap:
.
§2. Trigonometrik eşitsizlikleri çözmek için bir dizi problem
Okul çocuklarının trigonometrik eşitsizlikleri çözme becerilerini geliştirme sürecinde 3 aşama da ayırt edilebilir. 1. hazırlık, 2. Basit trigonometrik eşitsizlikleri çözme becerisinin geliştirilmesi; 3. Diğer türdeki trigonometrik eşitsizliklerin tanıtılması. Hazırlık aşamasının amacı, okul çocuklarında eşitsizlikleri çözmek için trigonometrik daire veya grafik kullanma becerisinin geliştirilmesinin gerekli olmasıdır: Formdaki basit eşitsizlikleri çözme becerisi Sayı çemberinin yayları veya fonksiyon grafiklerinin yayları için çift eşitsizlikler oluşturma becerisi; Trigonometrik ifadelerin çeşitli dönüşümlerini gerçekleştirebilme. Bu aşamanın, okul çocuklarının trigonometrik fonksiyonların özellikleri hakkındaki bilgilerini sistematikleştirme sürecinde uygulanması tavsiye edilir. Ana araçlar, öğrencilere sunulan ve bir öğretmenin rehberliğinde veya bağımsız olarak gerçekleştirilen görevlerin yanı sıra trigonometrik denklemleri çözmede geliştirilen beceriler olabilir. İşte bu tür görevlere örnekler: 1
. Birim çember üzerinde bir nokta işaretleyin .
2.
Nokta koordinat düzleminin hangi çeyreğinde yer alır? 3.
Trigonometrik çemberdeki noktaları işaretleyin 4.
İfadeyi trigonometrik fonksiyonlara dönüştürünBENçeyrekler. A) 5.
Ark MR verilir.M
- ortaBEN-inci çeyrek,R
- ortaIIçeyrek. Bir değişkenin değerini sınırlamaT
için: (çift eşitsizlik yapın) a) yay MR; b) RM yayları. 6.
Grafiğin seçilen bölümleri için çift eşitsizliği yazın: Pirinç. 1 7.
Eşitsizlikleri çözme 8.
İfadeyi Dönüştür
.
Trigonometrik eşitsizlikleri çözmeyi öğrenmenin ikinci aşamasında, öğrencilerin etkinliklerini düzenleme metodolojisine ilişkin aşağıdaki önerileri sunabiliriz. Bu durumda öğrencilerin en basit trigonometrik denklemleri çözerken oluşan trigonometrik daire veya grafikle çalışma konusundaki mevcut becerilerine odaklanmak gerekir. İlk olarak, en basit trigonometrik eşitsizlikleri çözmek için genel bir yöntem elde etmenin uygunluğunu, örneğin formun bir eşitsizliğine dönerek motive edebiliriz. İkinci olarak, öğretmen öğrencilerin dikkatini görevi tamamlamanın farklı yollarına çekmeli, eşitsizliği hem grafiksel olarak hem de trigonometrik çember kullanarak çözmenin uygun bir örneğini vermelidir. Eşitsizliğin aşağıdaki çözümlerini ele alalım 1. Birim çemberi kullanarak eşitsizliği çözme. Trigonometrik eşitsizliklerin çözümüne ilişkin ilk derste öğrencilere, eşitsizliği çözmek için gerekli tüm temel becerileri adım adım bir sunumla yansıtan ayrıntılı bir çözüm algoritması sunacağız. Adım 1.Birim çember çizelim ve ordinat ekseninde bir nokta işaretleyelim Adım 2.Bu düz çizgi daireyi iki yaya bölüyordu. Sinüs değeri bundan büyük olan sayıları göstereni seçelim. Pirinç. 2 Adım 3.İşaretli yayın uçlarından birini seçin. Birim çemberin bu noktasının temsil ettiği sayılardan birini yazalım. Adım 4.Seçilen yayın ikinci ucuna karşılık gelen sayıyı seçmek için bu yay boyunca adı geçen uçtan diğerine "yürüyeceğiz". Aynı zamanda saat yönünün tersine hareket ettiğimizde geçeceğimiz sayıların arttığını (ters yönde hareket ettiğimizde ise sayıların azaldığını) unutmayın. Birim çember üzerinde gösterilen sayıyı işaretli yayın ikinci ucuna yazalım. Böylece eşitsizliği görüyoruz. Öğrencilerden çizimi dikkatlice incelemeleri ve eşitsizliğin tüm çözümlerinin nedenini bulmaları istenmelidir. Pirinç. 3 Kosinüs fonksiyonu için eşitsizlikleri çözerken ordinat eksenine paralel düz bir çizgi çizdiğimize öğrencilerin dikkatini çekmek gerekir. Eşitsizliklerin çözümü için grafiksel yöntem. Grafikler oluşturuyoruz Pirinç. 4 Daha sonra denklemi yazıyoruz (VermekN
0, 1, 2 değerlerinde derlenmiş denklemin üç kökünü buluruz). Değerler Pirinç. 5 Özetleyelim. Eşitsizliği çözmek için Üçüncüsü, karşılık gelen trigonometrik eşitsizliğin kök kümesiyle ilgili gerçek, grafiksel olarak çözülürken çok açık bir şekilde doğrulanır. Pirinç. 6 Eşitsizliğin çözümü olan dönüşün trigonometrik fonksiyonun periyoduna eşit olan aynı aralıkta tekrarlandığını öğrencilere göstermek gerekir. Benzer bir çizimi sinüs fonksiyonunun grafiği için de düşünebilirsiniz. Dördüncü olarak, öğrencilerin trigonometrik fonksiyonların toplamını (farkını) çarpıma dönüştürme tekniklerinin güncellenmesine yönelik çalışmaların yapılması ve öğrencilerin dikkatini bu tekniklerin trigonometrik eşitsizliklerin çözümündeki rolüne çekmesi önerilir. Bu tür çalışmalar, öğrencilerin öğretmen tarafından önerilen görevleri bağımsız olarak tamamlamaları yoluyla organize edilebilir; bunların arasında aşağıdakileri vurguluyoruz: Beşinci olarak, öğrencilerden her basit trigonometrik eşitsizliğin çözümünü bir grafik veya trigonometrik daire kullanarak göstermeleri istenmelidir. Trigonometrik eşitsizlikleri çözerken, ilgili çizim belirli bir eşitsizliğin çözüm kümesini kaydetmenin çok uygun bir yolu olduğundan, özellikle dairenin kullanımına kesinlikle dikkat etmelisiniz. Öğrencilere, aşağıdaki şemaya göre en basit olmayan trigonometrik eşitsizlikleri çözme yöntemlerinin tanıtılması tavsiye edilir: belirli bir trigonometrik eşitsizliğe dönüş, karşılık gelen trigonometrik denkleme dönüş, bağımsız bir çözüm için ortak arama (öğretmen - öğrenciler) Aynı türdeki diğer eşitsizlikler için bulunan yöntem. Öğrencilerin trigonometri hakkındaki bilgilerini sistematize etmek için, çözümü, süreçte uygulanabilecek çeşitli dönüşümler gerektiren bu tür eşitsizliklerin özel olarak seçilmesini ve öğrencilerin dikkatinin özelliklerine odaklanmasını öneriyoruz. Bu tür üretken eşitsizlikler olarak örneğin aşağıdakileri önerebiliriz: Sonuç olarak trigonometrik eşitsizliklerin çözümüne yönelik bir dizi problemin örneğini veriyoruz. 1. Eşitsizlikleri çözün: A) B) 5. Eşitsizliklerin tüm çözümlerini bulun: A) ;
B) ;
V) G) D) 6. Eşitsizlikleri çözün: A) ;
B) ;
V) ; G) D) ; e) ; Ve) 7. Eşitsizlikleri çözün: A) B) ;
V) ; G) . 8. Eşitsizlikleri çözün: A) ;
B) ;
V) ; G) D) e) ; Ve) H) . İleri düzeyde matematik eğitimi alan öğrencilere Görev 6 ve 7'nin, ileri matematik eğitimi verilen sınıflardaki öğrencilere Görev 8'in sunulması tavsiye edilir. §3. Trigonometrik eşitsizlikleri çözmek için özel yöntemler
Trigonometrik denklemleri çözmek için özel yöntemler - yani yalnızca trigonometrik denklemleri çözmek için kullanılabilecek yöntemler. Bu yöntemler trigonometrik fonksiyonların özelliklerinin kullanılmasının yanı sıra çeşitli trigonometrik formüllerin ve özdeşliklerin kullanımına dayanmaktadır. 3.1. Sektör yöntemi
Trigonometrik eşitsizlikleri çözmek için sektör yöntemini ele alalım. Formdaki eşitsizlikleri çözme Aralık yönteminde formun pay ve paydasının her doğrusal faktörü Aşağıdakiler hatırlanmalıdır: a) Formun faktörleri b) Formun faktörleri Örnek 1.
Eşitsizlikleri çözün: a) 3.2. Eşmerkezli daire yöntemi
Bu yöntem, rasyonel eşitsizlik sistemlerini çözmek için paralel sayı eksenleri yönteminin bir analogudur. Eşitsizlik sisteminin bir örneğini ele alalım. Örnek 5.
Basit trigonometrik eşitsizlikler sistemini çözme Öncelikle her bir eşitsizliği ayrı ayrı çözüyoruz (Şekil 5). Şeklin sağ üst köşesinde trigonometrik çemberin hangi argüman için dikkate alındığını göstereceğiz. Şekil 5 Daha sonra, argüman için eşmerkezli dairelerden oluşan bir sistem oluşturuyoruzX
. Bir daire çizip onu birinci eşitsizliğin çözümüne göre gölgelendiriyoruz, sonra daha büyük yarıçaplı bir daire çizip onu ikincinin çözümüne göre gölgelendiriyoruz, sonra üçüncü eşitsizlik için bir daire ve bir taban daire oluşturuyoruz. Sistemin merkezinden gelen ışınları yayların uçlarından tüm çevrelerle kesişecek şekilde çekiyoruz. Taban çemberi üzerinde bir çözüm oluşturuyoruz (Şekil 6). Şekil 6 Cevap:
Çözüm
Kurs araştırmasının tüm hedefleri tamamlandı. Teorik materyal sistematik hale getirilmiştir: trigonometrik eşitsizliklerin ana türleri ve bunları çözmenin ana yöntemleri verilmiştir (grafik, cebir, aralık yöntemi, sektörler ve eşmerkezli daireler yöntemi). Her yöntem için bir eşitsizliğin çözümüne ilişkin bir örnek verilmiştir. Teorik kısmın ardından pratik kısıma geçildi. Trigonometrik eşitsizlikleri çözmek için bir dizi görev içerir. Bu kurs, öğrenciler tarafından bağımsız çalışmalar için kullanılabilir. Okul çocukları bu konudaki ustalık düzeylerini kontrol edebilir ve değişen karmaşıklıktaki görevleri tamamlama konusunda pratik yapabilirler. Bu konuyla ilgili ilgili literatürü inceledikten sonra, okul cebir ve temel analiz dersinde trigonometrik eşitsizlikleri çözme beceri ve becerilerinin çok önemli olduğu ve geliştirilmesinin matematik öğretmeni açısından önemli çaba gerektirdiği sonucuna varabiliriz. Bu nedenle, bu çalışma matematik öğretmenleri için faydalı olacaktır çünkü öğrencilerin “Trigonometrik eşitsizlikler” konusundaki eğitimlerini etkili bir şekilde organize etmeyi mümkün kılmaktadır. Araştırma, nihai bir niteleyici çalışmaya kadar genişletilerek devam ettirilebilir..
Kullanılmış literatür listesi
Bogomolov, N.V. Matematikte problemlerin toplanması [Metin] / N.V. Bogomolov. – M.: Bustard, 2009. – 206 s. Vygodsky, M.Ya. İlköğretim matematik el kitabı [Metin] / M.Ya. Vygodsky. – M.: Bustard, 2006. – 509 s. Zhurbenko, L.N. Örneklerde ve problemlerde matematik [Metin] / L.N. Zhurbenko. – M.: Infra-M, 2009. – 373 s. Ivanov, O.A. Okul çocukları, öğrenciler ve öğretmenler için ilköğretim matematik [Metin] / O.A. Ivanov. – M.: MTsNMO, 2009. – 384 s. Karp, A.P. 11. sınıfta son tekrar ve sertifikasyonun düzenlenmesi için cebir ve analizin başlangıcı üzerine ödevler [Metin] / A.P. Sazan. – M.: Eğitim, 2005. – 79 s. Kulanin, E.D. Matematikte 3000 rekabet problemi [Metin] / E.D. Kulanin. – M.: Iris-press, 2007. – 624 s. Leibson, K.L. Matematikte pratik görevlerin toplanması [Metin] / K.L. Leibson. – M.: Bustard, 2010. – 182 s. Dirsek, V.V. Parametrelerle ilgili problemler ve çözümleri. Trigonometri: denklemler, eşitsizlikler, sistemler. 10. sınıf [Metin] / V.V. Dirsek. – M.: ARKTI, 2008. – 64 s. Manova, A.N. Matematik. Birleşik Devlet Sınavına hazırlanmak için hızlı öğretmen: öğrenci. manuel [Metin] / A.N. Manova. – Rostov-na-Donu: Phoenix, 2012. – 541 s. Mordkovich, A.G. Cebir ve matematiksel analizin başlangıcı. 10-11 sınıflar. Genel eğitim kurumlarının öğrencileri için ders kitabı [Metin] / A.G. Mordkoviç. – M.: Iris-press, 2009. – 201 s. Novikov, A.I. Trigonometrik fonksiyonlar, denklemler ve eşitsizlikler [Metin] / A.I. Novikov. – M.: FİZMATLİT, 2010. – 260 s. Oganesyan, V.A. Ortaokulda matematik öğretme yöntemleri: Genel metodoloji. Ders Kitabı fizik öğrencileri için el kitabı - paspas. sahte. ped. Öğr. [Metin] / V.A. Oganesyan. – M.: Eğitim, 2006. – 368 s. Olehnik, S.N. Denklemler ve eşitsizlikler. Standart dışı çözüm yöntemleri [Metin] / S.N. Olehnik. – M.: Faktöriyel Yayınevi, 1997. – 219 s. Sevryukov, P.F. Trigonometrik, üstel ve logaritmik denklemler ve eşitsizlikler [Metin] / P.F. Sevryukov. – M.: Halk Eğitimi, 2008. – 352 s. Sergeyev, I.N. Birleşik Devlet Sınavı: Matematikte cevapları ve çözümleri olan 1000 problem. C grubunun tüm görevleri [Metin] / I.N. Sergeyev. – M.: Sınav, 2012. – 301 s. Sobolev, A.B. İlköğretim matematik [Metin] / A.B. Sobolev. – Ekaterinburg: Yüksek Mesleki Eğitim Devlet Eğitim Kurumu USTU-UPI, 2005. – 81 s. Fenko, L.M. Eşitsizliklerin çözümünde ve fonksiyonların incelenmesinde aralık yöntemi [Metin] / L.M. Fenko. – M.: Bustard, 2005. – 124 s. Friedman, L.M. Matematik öğretme yöntemlerinin teorik temelleri [Metin] / L.M. Friedman. – M.: Kitapevi “LIBROKOM”, 2009. – 248 s. Ek 1 Basit eşitsizliklerin çözümlerinin grafiksel yorumu Pirinç. 1 Pirinç. 2 Şekil 3 Şekil 4 Şekil 5 Şekil 6 Şekil 7 Şekil 8 Ek 2 Basit eşitsizliklerin çözümleri Basit trigonometrik eşitsizlikleri çözmeye yönelik bir algoritma ve trigonometrik eşitsizlikleri çözmeye yönelik yöntemleri tanıyan bir algoritma. En yüksek yeterlilik kategorisindeki öğretmenler: Shirko F.M. s. İlerleme, MOBU-SOSH No. 6 Sankina L.S. Armavir, özel ortaokul "Yeni Yol" Fen ve matematik disiplinlerini öğretmek için evrensel bir yöntem yoktur. Her öğretmen yalnızca kendisi için kabul edilebilir olan kendi öğretme yollarını bulur. Uzun yıllara dayanan öğretme deneyimimiz, öğrencilere karmaşık bir konuyu öğrenmenin ilk aşamasında etkinliklerinde algoritmaları kullanmaları öğretilirse, büyük miktarda bilginin konsantrasyonunu ve hafızada tutulmasını gerektiren materyalleri daha kolay öğrendiklerini göstermektedir. Bizce böyle bir konu trigonometrik eşitsizliklerin çözümü konusudur. Bu nedenle, öğrencilerle trigonometrik eşitsizlikleri çözmeye yönelik teknikleri ve yöntemleri belirlemeye başlamadan önce, en basit trigonometrik eşitsizlikleri çözmek için bir algoritma uygular ve pekiştiririz. Basit trigonometrik eşitsizlikleri çözmek için algoritma
İlgili eksendeki noktaları işaretleyin ( İçin
günah
X– OA ekseni,çünkü
X– OX ekseni) Çemberi iki noktada kesecek eksene dik olanı geri getiriyoruz. Çember üzerindeki ilk nokta, tanımı gereği yay fonksiyonu aralığının aralığına ait olan bir noktadır. Etiketli noktadan başlayarak, eksenin gölgeli kısmına karşılık gelen dairenin yayını gölgelendirin. Dönüş yönüne özellikle dikkat ediyoruz. Eğer geçiş saat yönünde yapılırsa (yani 0'dan geçiş varsa), o zaman çember üzerindeki ikinci nokta negatif, saat yönünün tersine ise pozitif olacaktır. Cevabı, fonksiyonun periyodikliğini dikkate alarak aralık şeklinde yazıyoruz. Örnekler kullanarak algoritmanın işleyişine bakalım.
1)
günah
≥ 1/2;
Çözüm: Birim çemberi tasvir ediyoruz; OU ekseninde ½ noktasını işaretliyoruz. Eksene dik olanı geri getiriyoruz, çemberi iki noktada kesen nokta. Arksinüsün tanımı gereği, ilk olarak şunu not ediyoruz: nokta π/6. Eksenin karşılık gelen kısmını gölgelendirin eşitsizlik verildiğinde, ½ noktasının üzerinde. Eksenin gölgeli kısmına karşılık gelen dairenin yayını gölgelendirin. Çaprazlama saat yönünün tersine yapılırsa 5π/6 noktasını elde ederiz. Cevabı, fonksiyonun periyodikliğini dikkate alarak aralık şeklinde yazıyoruz; Cevap:X;[π/6 + 2π N, 5π/6 + 2π N], NZ. En basit eşitsizlik, cevap kaydının bir tablo değeri içermemesi durumunda aynı algoritma kullanılarak çözülür. Öğrenciler ilk derslerinde tahtada eşitsizlikleri çözerken algoritmanın her adımını yüksek sesle okurlar. 2) 5
çünkü
X
– 1 ≥ 0;
R 5 çünkü X – 1 ≥ 0; çünkü
X ≥ 1/5; Bir birim çember çizin. OX ekseninde koordinatı 1/5 olan bir noktayı işaretliyoruz. Eksene dik olanı geri yüklüyoruz; çemberi iki noktada keser. Çember üzerindeki ilk nokta, tanım gereği (0;π) yay kosinüs aralığının aralığına ait olan bir noktadır. Eksenin bu eşitsizliğe karşılık gelen kısmını gölgeliyoruz. İmzalı noktadan başlayarak
Arcco'lar 1/5, eksenin gölgeli kısmına karşılık gelen dairenin yayını gölgelendirin. Geçiş saat yönünde yapılır (yani 0'dan geçiş vardır), bu da daire üzerindeki ikinci noktanın negatif olacağı anlamına gelir - Arcco'lar 1/5. Cevabı, fonksiyonun periyodikliğini dikkate alarak, küçük değerden büyüğe doğru bir aralık şeklinde yazıyoruz. Cevap: X [-Arcco'lar 1/5 + 2π N, Arcco'lar 1/5 + 2π N], NZ. Trigonometrik eşitsizlikleri çözme yeteneğinin geliştirilmesi aşağıdaki sorularla kolaylaştırılmıştır: "Bir grup eşitsizliği nasıl çözeceğiz?"; “Bir eşitsizlik diğerinden nasıl farklıdır?”; “Bir eşitsizlik diğerine nasıl benzer?”; Tam eşitsizlik verildiğinde cevap nasıl değişirdi?"; "" İşareti yerine bir işaret olsaydı cevap nasıl değişirdi? Eşitsizliklerin bir listesini bunları çözme yöntemleri açısından analiz etme görevi, bunların tanınması konusunda pratik yapmanızı sağlar. Öğrencilere sınıfta çözülmesi gereken eşitsizlikler verilir. Soru: Trigonometrik bir eşitsizliği en basit biçimine indirirken eşdeğer dönüşümlerin kullanılmasını gerektiren eşitsizlikleri vurgulayın? Cevap 1, 3, 5. Soru: Karmaşık bir argümanı basit bir argüman olarak değerlendirmenizi gerektiren eşitsizlikler nelerdir? Cevap: 1, 2, 3, 5, 6. Soru: Trigonometrik formüllerin uygulanabileceği eşitsizlikler nelerdir? Cevap: 2, 3, 6. Soru: Yeni bir değişken ekleme yönteminin uygulanabileceği eşitsizlikleri adlandırın? Cevap: 6. Eşitsizliklerin bir listesini bunları çözme yöntemleri açısından analiz etme görevi, bunların tanınması konusunda pratik yapmanızı sağlar. Becerileri geliştirirken, uygulama aşamalarını belirlemek ve bunları en basit trigonometrik eşitsizlikleri çözmek için algoritmada sunulan genel bir biçimde formüle etmek önemlidir.Yöntem 1 - Bir fonksiyonun grafiğini çizerek eşitsizlikleri çözme
![]()
![]()
Yöntem 2 - Birim çemberi kullanarak trigonometrik eşitsizlikleri çözme
![]()





Karmaşık trigonometrik eşitsizlikler



Eşitsizlikleri sinüsle çözmek için algoritma:
Algoritma sınırlaması
Eşitsizlikleri sinüsle çözerken özel durumlar
Bir algoritma kullanarak eşitsizlikleri çözme örnekleri.






 Dolayısıyla bu eşitsizliğin çözümü aralık olacaktır:
Dolayısıyla bu eşitsizliğin çözümü aralık olacaktır:
 ,
,  vb.), burada olağan eşitsizlik ilk önce çözülür ve ardından formun eşitsizliği
vb.), burada olağan eşitsizlik ilk önce çözülür ve ardından formun eşitsizliği  vb. veya diğer yöntemler.
vb. veya diğer yöntemler. çözümünü bir dönemde bulmak yeterlidir, yani. uzunluğu fonksiyonun periyoduna eşit olan herhangi bir parça üzerindeF
X
. O zaman orijinal eşitsizliğin çözümü bulunacakX
fonksiyonun herhangi bir tamsayı periyodu tarafından bulunan değerlerden farklı olan değerlerin yanı sıra. Bu durumda grafik yönteminin kullanılması uygundur.
çözümünü bir dönemde bulmak yeterlidir, yani. uzunluğu fonksiyonun periyoduna eşit olan herhangi bir parça üzerindeF
X
. O zaman orijinal eşitsizliğin çözümü bulunacakX
fonksiyonun herhangi bir tamsayı periyodu tarafından bulunan değerlerden farklı olan değerlerin yanı sıra. Bu durumda grafik yönteminin kullanılması uygundur. (
(
 ) Ve
) Ve  .
.
 (
(
 ).
).
 .
.
 .
.
 (girişin solundaki sayı her zaman sağındaki sayıdan küçüktür).
(girişin solundaki sayı her zaman sağındaki sayıdan küçüktür). .
.
 çemberi A ve B noktalarında kesen noktadır.
çemberi A ve B noktalarında kesen noktadır. , ama daha küçük
, ama daha küçük  ,
,
 daha büyük değerlere bürünecek
(ancak birden fazla değil).
daha büyük değerlere bürünecek
(ancak birden fazla değil).
 yani
yani  . Bu eşitsizliğin tüm çözümlerini elde etmek için bu aralığın uçlarına ekleme yapmak yeterlidir.
. Bu eşitsizliğin tüm çözümlerini elde etmek için bu aralığın uçlarına ekleme yapmak yeterlidir.  , Nerede
, Nerede  yani
yani  ,
,
 .
Değerlere dikkat edin
.
Değerlere dikkat edin  Ve
Ve  denklemin kökleri
denklemin kökleri  ,
,
 ;
;
 .
.
 ,
,  .
.
 :
:
 Ve
Ve  .
.
 . Bu noktaların apsislerini buluyoruz.
. Bu noktaların apsislerini buluyoruz.
 Ve
Ve  (Şekil 2).
(Şekil 2).
 ;
;  . Arasında
. Arasında  grafik noktaları
grafik noktaları  grafik noktalarının altında
grafik noktalarının altında  . Ve ne zaman
. Ve ne zaman  fonksiyon değerleri aynıdır. Bu yüzden
fonksiyon değerleri aynıdır. Bu yüzden  en
en  .
.
 .
.
 .
.

 (Şekil 3)
(Şekil 3)

 ,
,  .
.

 ,
, 
 ,
,  .
.
 ,
, 
 .
.
 basit dönüşümlerden sonra elde ederiz
basit dönüşümlerden sonra elde ederiz ,
,
 ,
,
 .
.

 sırasıyla
sırasıyla  . Daha sonra Şek. 4 takip
. Daha sonra Şek. 4 takip  , Nerede
, Nerede  .
.

 ,
,  .
.
 ,
,  .
.
 .
.
 .
.
 : . Birim çember üzerindeki tüm noktaları işaretleyelim (Şekil 6):
: . Birim çember üzerindeki tüm noktaları işaretleyelim (Şekil 6):
 ,
,  ;
;  ,
,  ;
;  ,
,  .
.
 ,
,
 ;
;
 ,
,  ;
;
 ,
,  ;
;
 ,
,  ;
;
 . SeriX
2
puan verir
. SeriX
2
puan verir  . SeridenX
3
iki puan aldık
. SeridenX
3
iki puan aldık  . Son olarak diziX
4
noktaları temsil edecek
. Son olarak diziX
4
noktaları temsil edecek  . Tüm bu noktaları birim çember üzerinde işaretleyelim ve bunların çokluğunu her birinin yanında parantez içinde belirtelim.
. Tüm bu noktaları birim çember üzerinde işaretleyelim ve bunların çokluğunu her birinin yanında parantez içinde belirtelim. eşit olacaktır. İşarete göre bir tahmin yapalım:
eşit olacaktır. İşarete göre bir tahmin yapalım:
 kirişliAh,
birim çemberin dışında. (Yardımcı ışınınHAKKINDA
A
Bir resimde tasvir etmek hiç de gerekli değildir. NoktaA
yaklaşık olarak seçilmiştir.)
kirişliAh,
birim çemberin dışında. (Yardımcı ışınınHAKKINDA
A
Bir resimde tasvir etmek hiç de gerekli değildir. NoktaA
yaklaşık olarak seçilmiştir.) doğrumuz bir alandan diğerine gider: eğer birim çemberin dışındaysa, o zaman onun içine girer. Noktaya yaklaşıyoruz
doğrumuz bir alandan diğerine gider: eğer birim çemberin dışındaysa, o zaman onun içine girer. Noktaya yaklaşıyoruz  Bu noktanın çokluğu çift olduğundan doğru iç bölgeye döner. Aynı noktada
Bu noktanın çokluğu çift olduğundan doğru iç bölgeye döner. Aynı noktada  (hatta çoklukla) hattın dış bölgeye çevrilmesi gerekiyor. Böylece, Şekil 2'de gösterilen belirli bir resmi çizdik. 7. Birim çember üzerinde istenilen alanların vurgulanmasına yardımcı olur. “+” işaretiyle işaretlenmiştir.
(hatta çoklukla) hattın dış bölgeye çevrilmesi gerekiyor. Böylece, Şekil 2'de gösterilen belirli bir resmi çizdik. 7. Birim çember üzerinde istenilen alanların vurgulanmasına yardımcı olur. “+” işaretiyle işaretlenmiştir.
 ,
,
 ,
,  ,
,
 ,
sinüs ve kosinüs fonksiyonlarının özelliklerinin kullanılması;
,
sinüs ve kosinüs fonksiyonlarının özelliklerinin kullanılması; , Eğer
, Eğer , Eğer
, Eğer  eşittir:
eşittir: 
 , Eğer:
, Eğer:
 ,
B)
,
B)  ,
V)
,
V) 

 ,
,  ,
,  ,
,  .
.
 .
Hazırlık aşamasında edinilen bilgi ve becerileri kullanarak öğrenciler önerilen eşitsizliği forma getireceklerdir.
.
Hazırlık aşamasında edinilen bilgi ve becerileri kullanarak öğrenciler önerilen eşitsizliği forma getireceklerdir.  ancak ortaya çıkan eşitsizliğe bir dizi çözüm bulmak zor olabilir çünkü Bunu yalnızca sinüs fonksiyonunun özelliklerini kullanarak çözmek imkansızdır. Bu zorluk, uygun resme dönülerek (denklemin grafiksel olarak çözülmesi veya birim daire kullanılarak) önlenebilir.
ancak ortaya çıkan eşitsizliğe bir dizi çözüm bulmak zor olabilir çünkü Bunu yalnızca sinüs fonksiyonunun özelliklerini kullanarak çözmek imkansızdır. Bu zorluk, uygun resme dönülerek (denklemin grafiksel olarak çözülmesi veya birim daire kullanılarak) önlenebilir. .
.
 ve içinden x eksenine paralel düz bir çizgi çizin. Bu doğru birim çemberi iki noktada kesecektir. Bu noktaların her biri sinüsü eşit olan sayıları temsil eder.
ve içinden x eksenine paralel düz bir çizgi çizin. Bu doğru birim çemberi iki noktada kesecektir. Bu noktaların her biri sinüsü eşit olan sayıları temsil eder.  .
.
 . Doğal olarak bu yay çizilen düz çizginin üzerinde bulunur.
. Doğal olarak bu yay çizilen düz çizginin üzerinde bulunur.
 .
.
 .
.
 eşitsizliğin doğru olduğu sayıları karşılayın
eşitsizliğin doğru olduğu sayıları karşılayın  . Sinüs fonksiyonunun aynı periyodunda bulunan sayılar için eşitsizliği çözdük. Bu nedenle eşitsizliğin tüm çözümleri şu şekilde yazılabilir:
. Sinüs fonksiyonunun aynı periyodunda bulunan sayılar için eşitsizliği çözdük. Bu nedenle eşitsizliğin tüm çözümleri şu şekilde yazılabilir: ![]()
 şeklinde yazılabilir
şeklinde yazılabilir  ,
,  .
.

 Ve
Ve  , buna göre
, buna göre  .
.

 ve onun kararı
ve onun kararı  ,
,  ,
,  , formüller kullanılarak bulundu
, formüller kullanılarak bulundu  ,
,  ,
,  .
.
 grafiklerin kesişme noktalarının ardışık üç apsisidir
grafiklerin kesişme noktalarının ardışık üç apsisidir  Ve
Ve  . Açıkçası, her zaman aralıkta
. Açıkçası, her zaman aralıkta  eşitsizlik geçerli
eşitsizlik geçerli  ve aralıkta
ve aralıkta  – eşitsizlik
– eşitsizlik  . İlk durumla ilgileniyoruz ve sonra bu aralığın uçlarına sinüs periyodunun katı olan bir sayı ekleyerek eşitsizliğin çözümünü elde ediyoruz
. İlk durumla ilgileniyoruz ve sonra bu aralığın uçlarına sinüs periyodunun katı olan bir sayı ekleyerek eşitsizliğin çözümünü elde ediyoruz  formda:
formda:  ,
,  .
.

 , karşılık gelen denklemi oluşturup çözmeniz gerekir. Ortaya çıkan formülden kökleri bulun
, karşılık gelen denklemi oluşturup çözmeniz gerekir. Ortaya çıkan formülden kökleri bulun  Ve
Ve  ve eşitsizliğin cevabını forma yazın: ,
ve eşitsizliğin cevabını forma yazın: ,  .
.


![]()
![]()
 , koşulu karşılayan
, koşulu karşılayan  ;
;
 , koşulu karşılayan
, koşulu karşılayan  .
.
 ;
;
 ;
;
 .
.
 ;
;
 .
.
 ;
;
 ;
;
 ;
;
 ;
;

 , NeredeP
(
X
)
VeQ
(
X
)
– rasyonel eşitsizliklerin çözümüne benzer şekilde rasyonel trigonometrik fonksiyonlar (sinüsler, kosinüsler, teğetler ve kotanjantlar rasyonel olarak bunlara dahil edilir). Rasyonel eşitsizlikleri sayı doğrusunda aralıklar yöntemini kullanarak çözmek uygundur. Rasyonel trigonometrik eşitsizlikleri çözmek için kullanılan analog, trigonometrik çemberdeki sektörlerin yöntemidir.sinx
Vecosx
(
, NeredeP
(
X
)
VeQ
(
X
)
– rasyonel eşitsizliklerin çözümüne benzer şekilde rasyonel trigonometrik fonksiyonlar (sinüsler, kosinüsler, teğetler ve kotanjantlar rasyonel olarak bunlara dahil edilir). Rasyonel eşitsizlikleri sayı doğrusunda aralıklar yöntemini kullanarak çözmek uygundur. Rasyonel trigonometrik eşitsizlikleri çözmek için kullanılan analog, trigonometrik çemberdeki sektörlerin yöntemidir.sinx
Vecosx
( ) veya trigonometrik yarım dairetgx
Vectgx
(
) veya trigonometrik yarım dairetgx
Vectgx
(
 ).
).
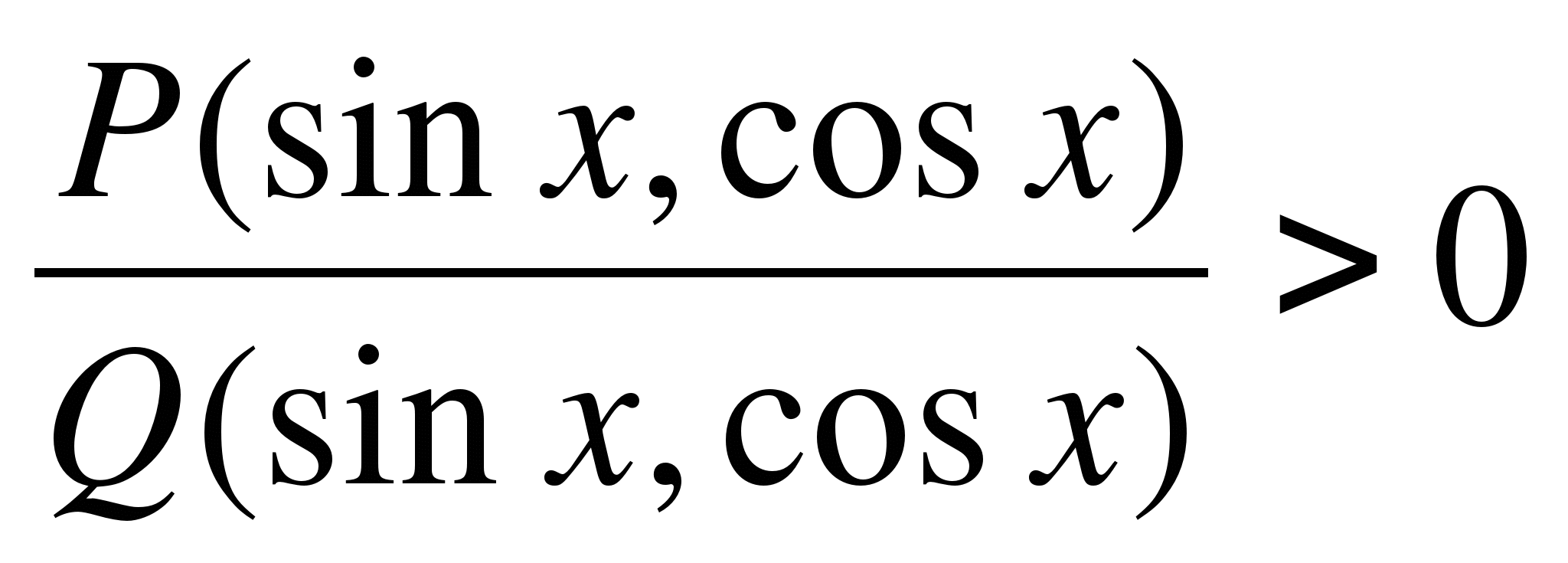
 sayı ekseninde bir noktaya karşılık gelir
sayı ekseninde bir noktaya karşılık gelir  ve bu noktadan geçerken
ve bu noktadan geçerken  işareti değiştirir. Sektör yönteminde formun her faktörü
işareti değiştirir. Sektör yönteminde formun her faktörü  , Nerede
, Nerede  - işlevlerden birisinx
veyacosx
Ve
- işlevlerden birisinx
veyacosx
Ve  Trigonometrik bir dairede iki açıya karşılık gelir
Trigonometrik bir dairede iki açıya karşılık gelir  Ve
Ve 
 Çemberi iki sektöre bölen. İçinden geçerken
Çemberi iki sektöre bölen. İçinden geçerken  Ve
Ve  işlev
işlev  işareti değiştirir.
işareti değiştirir. Ve
Ve  , Nerede
, Nerede  , tüm değerler için işareti koru
, tüm değerler için işareti koru  . Pay ve paydanın bu faktörleri değiştirilerek atılır (eğer
. Pay ve paydanın bu faktörleri değiştirilerek atılır (eğer  ) bu tür her reddetmede eşitsizlik işareti tersine çevrilir.
) bu tür her reddetmede eşitsizlik işareti tersine çevrilir. Ve
Ve  da atılır. Ayrıca, eğer bunlar paydanın faktörleri ise, formdaki eşitsizlikler eşdeğer eşitsizlikler sistemine eklenir.
da atılır. Ayrıca, eğer bunlar paydanın faktörleri ise, formdaki eşitsizlikler eşdeğer eşitsizlikler sistemine eklenir.  Ve
Ve  . Bunlar payın faktörleri ise, o zaman eşdeğer kısıtlama sisteminde eşitsizliklere karşılık gelirler.
. Bunlar payın faktörleri ise, o zaman eşdeğer kısıtlama sisteminde eşitsizliklere karşılık gelirler.  Ve
Ve  katı bir başlangıç eşitsizliği ve eşitlik durumunda
katı bir başlangıç eşitsizliği ve eşitlik durumunda  Ve
Ve  katı olmayan bir başlangıç eşitsizliği durumunda. Çarpanı atarken
katı olmayan bir başlangıç eşitsizliği durumunda. Çarpanı atarken  veya
veya  eşitsizlik işareti ters çevrilir.
eşitsizlik işareti ters çevrilir. , B)
, B)  .
b) fonksiyonumuz var. Elimizdeki eşitsizliği çözelim,
.
b) fonksiyonumuz var. Elimizdeki eşitsizliği çözelim,


 ,
,  .
.














 çözüm:en
çözüm:en





